接線係数理論による曲げ座屈荷重,

ここに,Etは接線弾性係数とよばれ,次のように定義される.

等価係数理論による曲げ座屈荷重,

ここに,Erは等価弾性係数とよばれ,次式より求まる.

It,Iuはそれぞれ座屈に伴って生じる曲げ応力が圧縮応力である部分(応力増加領域),引張応力である部分(応力現象領域)の座屈時の中立軸まわりの断面二次モーメントである.座屈時の中立軸の位置は次式から決まる.
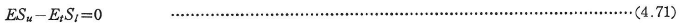
St,Suは座屈によって生じる曲げ応力がそれぞれ圧縮応力,引張応力である部分の座屈時の中立軸に関する断面一次モーメントである.
長方形断面の柱の等価弾性係数,

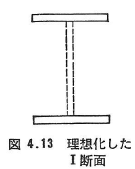
腹板断面積が無視され,フランジのみでできている理想化されたI断面柱(図4.13)の等価弾性係数,

非弾性域におけるねじり座屈,ねじり変位と曲げ変位が達成する座屈に対して,弾性座屈式の縦弾性係数,せん断弾性係数をそれぞれの接線弾性係数で置き換えることによって接線係数理論による座屈荷重が求まる.
