式（8.6）や式（8.11）は端モーメントと変形との関係を示した式であるが，これを用いて各部材の変形どうしの連続条件を満たしつつ，つり合い式をたてて，未知の変形を求めれば，構造全体が解ける．
　たわみ角法における連続条件とは，節点における部材どうしの交角が変形後も変化しないことを意味する．すなわち，一節点において，ある一部材がたわみ角θだけ回転すると，ほかの部材もやはりθだけ回転することになる．したがって，図8.9(a)のようなラーメンを考えると，図(b)に示すように，節点Aに集まる部材の未知のたわみ角をすべて節点（回転）角θ_Aに等しくて方程式をたてると自動的に連続条件（剛結条件）は満足されることになる．

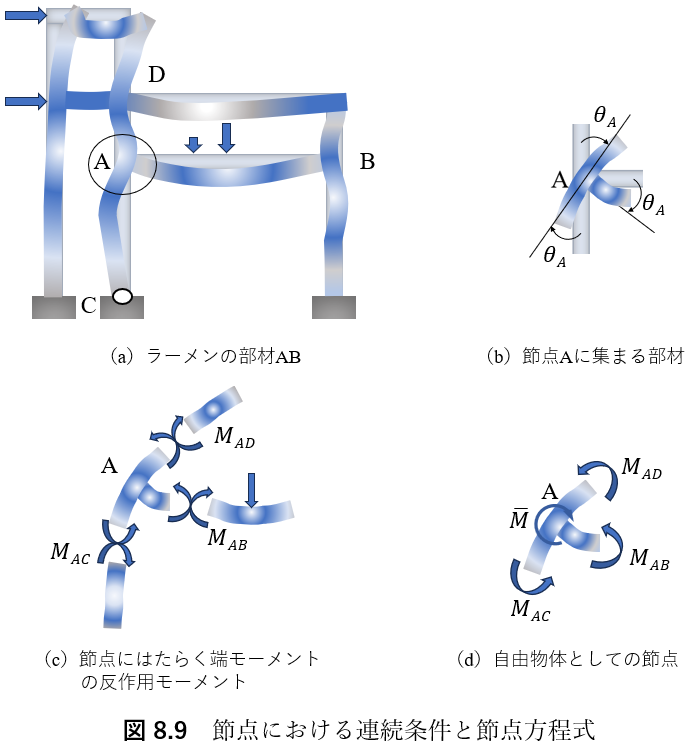
　次に，節点におけるモーメントのつり合い条件式を求める．端モーメントは，部材へはたらきかけるモーメントであり，図8.9(c)に示すように，節点は部材から大きさが等しく向きが反対のモーメントを受けて回転を起こそうとする．いま，図(d)に示すように，時計まわりの外力モーメントが節点Aにはたらく場合（=0でもよい）を考えると，節点Aは自由物体として回転せずに静止している必要があるから，節点Aに集まる部材の端モーメントと，外力モーメントとはつり合わなければならない．すなわち

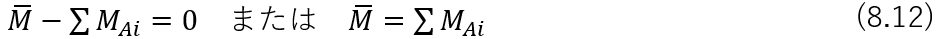
である．この式を節点方程式といい，節点ごとに一つずつ書けるから，未知数である節点角θの数に一致する数の方程式が得られることになる．
　節点方程式は，問題を解くため，式（8.12）を丸覚えすると符号を間違えやすい．図8.9(c)，(d)に示すように，端モーメントの反作用として節点の側に作用するモーメント（反時計まわりが正）に対して節点が自由物体として回転しない条件であるという意味を理解して，自分で式をつくれば符号を間違わない．