Contents
4.6.1 二軸対称断面柱
二軸対称断面柱では,二主軸に関する曲げ座屈とねじり座屈がそれぞれ独立し,この3つの座屈荷重のうちのもっとも小さな荷重が座屈荷重となる.等断面柱のねじり座屈荷重は次のように表される.
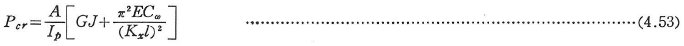
ここに,Kxはねじり座屈に対する有効座屈係数であり境界条件によって決まる.有効長さ係数の値は,境界条件に応じて対応する曲げ座屈に対する有効長さ係数の値をそのまま用いてよい.
4.6.2 一軸対称断面柱
一軸対称断面柱では,対象軸と直交する方向に変位する曲げ座屈とねじり座屈とが達成して生じ,子の座屈と,対象軸方向に変位する曲げ座屈の2つの独立した座屈荷重が存在する.z軸が断面の対象軸のとき,z軸直角方向への曲げ変位とねじり変位とが達成して生じる座屈形式の座屈荷重は,次式で表される.
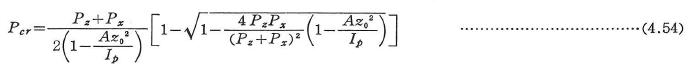
ここに,

z0はせん断中心の座標である.
4.6.3 非対称断面柱
対象軸のない断面の柱では二主軸方向への曲げ変位とねじり変位とが達成して生じる.子の座屈形式が唯一の座屈形式となり,次の三次式の最小限が座屈荷重となる.
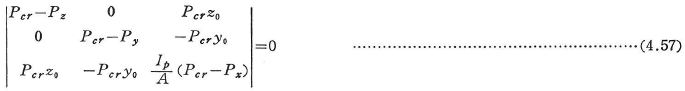
ここに,

(y0,z0)はせん断中心の座標である.
4,6,4 連続的に弾性支持された柱の曲げねじり座屈
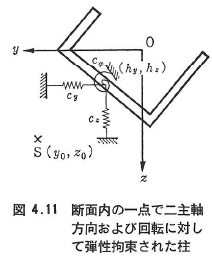
柱断面内の一点で二主軸方向並びに回転に対して弾性支持されており(図4.11),長さ方向にはこの支持状態が連続している柱の座屈荷重は,断面の形状およびばねの位置によって次のように表される.
(a)両端で単純に支持された二軸対称断面柱の重心点にばねが作用
この場合には二主軸方向の曲げ座屈とねじり座屈は独立し,曲げ座屈荷重は式(4.24)で求められる.ねじり座屈荷重は次のように表される.
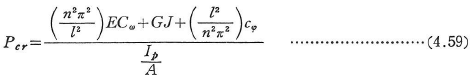
ここに,nは整数であり,座屈荷重を最小にする値を選ばねばならない.
(b)両端で単純支持された一軸対称断面柱でばねはせん断中心に作用
この場合には独立な座屈形式は対象軸方向に変位する曲げ座屈と,対象軸と直交する方向への曲げ変位とねじり変位が達成する座屈の2つとなり,前者の座屈荷重は式(4.24)により求まる.y軸を対象軸としたとき,曲げとねじりの達成する形式の座屈荷重は次の行列式の最小限として求められる.
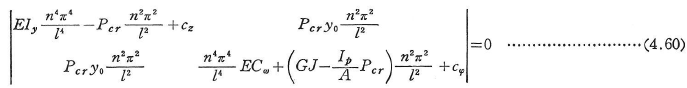
nは整数であり座屈荷重を最小にするように選ぶ.
(c)両端単純支持の固定した回転軸まわりの座屈
二軸対称断面柱の回転軸(hy,hz)のまわりの座屈荷重は,
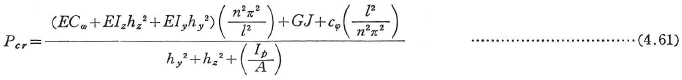
一般の断面を有する柱がせん断中心軸を回転軸として座屈するときの座屈荷重は,
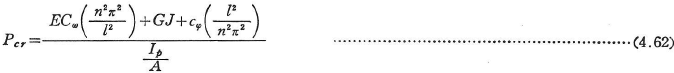
式(4.61),(4.62)においてnはいずれも整数であり,座屈荷重を最小にするように選ぶ.
(d)両端が単純支持され,一定の方向への変位が拘束された柱の座屈
断面内に重心を原点とするyz座標を考え,変位が拘束されている方向にy軸を選ぶ(図4.12).図中のN点でy方向への変位が拘束されているものとする.この柱の座屈荷重は次の行列式の最小根として求められる.
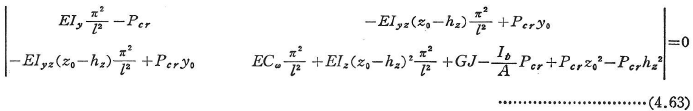
図4.12の断面において,z軸が対象軸となっておりN点が対象軸上にある場合の座屈荷重は次のように表される.
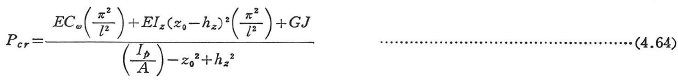
4.6.5 偏心軸圧縮を受ける柱の曲げねじり座屈
少なくとも,1つの対象軸を有する断面でできた柱が対象軸上に両端で偏心量の等しい載荷を受けているときの曲げねじり座屈荷重は次式の最小根として求まる.z軸を対象軸としたとき,
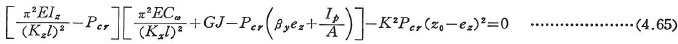
ここに,

Kz,Kx,Kは境界条件によって決まる係数であり表4.6に示す.表中,ω’=0,ω”=0はねじりに対して固定支持,単純支持の境界条件を表す.二軸対称断面ではβy=z0=0となる.