撓性マトリクスより剛性マトリクスのほうが容易に求められるので,以下では剛性マトリクスの求め方とその結果を示す.
図6.4(a)に示すバネ要素(バネ要素k)の剛性マトリクスを,つり合い式より求める.両端の節点1,2に作用するx軸方向の節点力x1,x2と,x軸方向変位u1,u2の関係を求めればよい.変位および節点力の正方向は,どちらの節点に関するものも,座標軸xの正方向に一致する向きとする.ここで,図(b)に示すように,節点1の右,節点2の左で切断すると,断面には,バネの伸び(u2-u1)によって軸力Nが生じており,バネ定数をkとすると N=k(u2-u1) となる.

節点1の力のつり合いを考えると
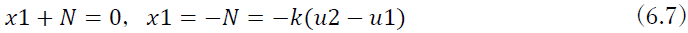
同様に節点2の力のつり合いを考えると
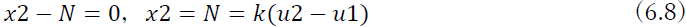
となり,この2式を行列表示すると
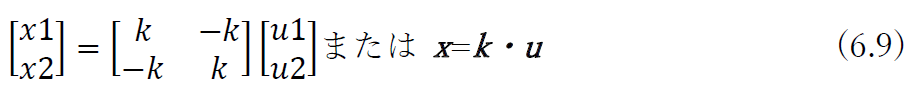
となる.ここで,kが剛性マトリクスであるが,![]() を節点力ベクトル,
を節点力ベクトル,![]() を(節点)変位ベクトルという.
を(節点)変位ベクトルという.
次に,図6.5(a)に示すように,バネ定数がそれぞれka,kbである2本のバネa,bを直列に連結した複合バネの剛性マトリクスを導いてみよう.

節点1の右,節点2の左右,節点3の左で切断して,図(b)のような自由物体図を描く.ここで,各節点節点力をx1,x2,x3,x軸方向変位をu1,u2,u3とし,バネaの軸力をNa,バネbの軸力をNbとすると,バネaについて,

バネbについて,

となる.次に,節点1のつり合いを考えると,
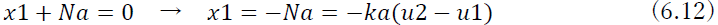
となる.同様に,節点2,3のつり合いを考えると,それぞれ
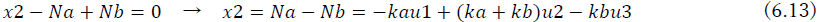
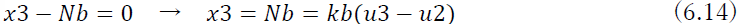
となる.
式(6.12)~(6.14)を行列表示すると
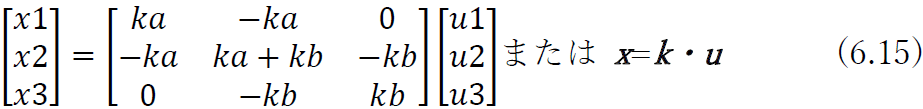
となる.
ところで,この剛性マトリクスkは,バネa,bをそれぞれ単独に考えると,式(6.9)で求められた単一バネの剛性マトリクスを足し合わせることによりつくり出せる.すなわち,バネaの剛性マトリクス
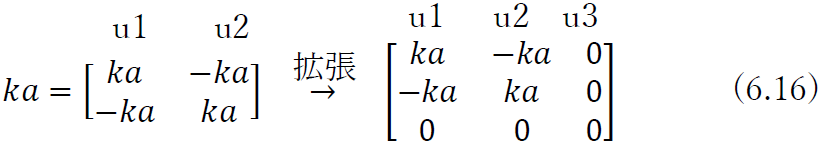
と,バネbの剛性マトリクス
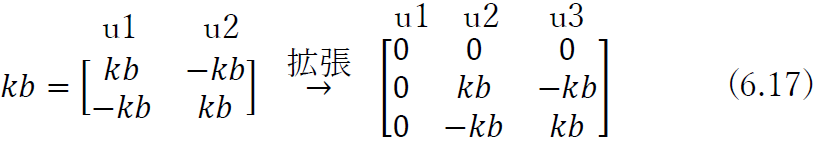
を足し合わせて
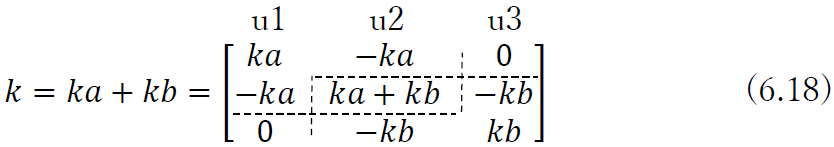
として得られる.以上の手順の意味を考えるために,図6.5(a)と同じ複合バネを図6.6に示すように二つのバネに分け,式(6.9)を利用して,バネaとバネbの剛性方程式をたてると

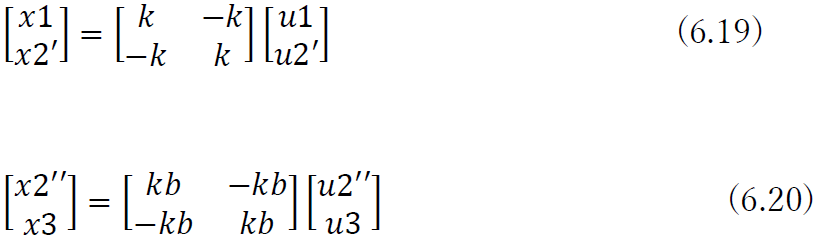
となる.ここで,図6.5(a)と同じ構造にするために,節点2’と節点2”を結合して,節点2とよぶことにすると

と書ける.これは隣接部材の節点変位の連続(適合)条件を表している.このとき,節点力も図(a)の節点2と同じになるためには

となればよい.これは,節点におけるつり合い条件になっている.以上を整理すれば,式(6.15)が得られる.すなわち,式(6.19)の1行目の式にu2’=u2を考慮すると

となる.次に式(6.19)の2行目の式と,式(6.20)の1行目の式を,式(6.22)に代入して
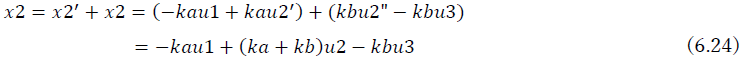
となる.また,式(6.20)の2行目の式にu2”=u2を考慮すると

となる.式(6.23)~(6.25)を行列表示すると,式(6.15)と同じ次式を得る.
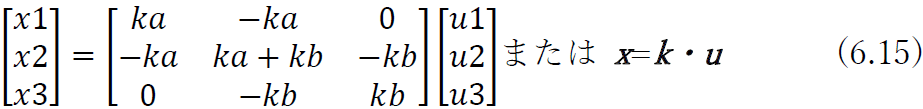
以下の考慮より式(6.16)~(6.18)の手順は,式(6.21)で表される節点での変位の適合条件(連続条件)と,式(6.22)で表される節点での力のつり合い条件を満足しつつ,部材同士を結合していくことを意味している.すなわち,一つの節点にいくつもの部材が集まるような複雑な構造物の剛性マトリクスでも,個々の部材の剛性マトリクスさえ得られれば,これを単純に重ね合わせ,足し合わせることによりつくり出すことができる.このことは,有限要素法にも共通する剛性マトリクスの最重要な性質であり,機械的なコンピュータ演算に適する最大の理由である.
部材の断面力を節点変位の関数として表した行列を応力マトリクスと名付けると,応力マトリクスは

を行列表示して
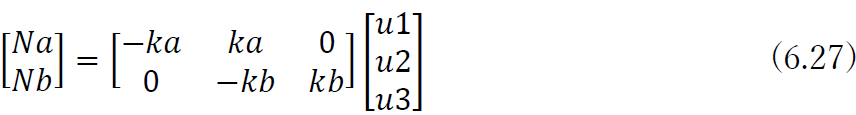
となる.
ここで,演習問題6.1を解いてみよう.⇒malme.app/news/演習問題/
さらに,剛性マトリクスには,このほかにも,以下のような性質がある.
- 対象マトリクスである:式(6.15)にみるように,主対角要素に対して対称な位置の要素は互いに等しい.これは,式(6.2)において,「点1の荷重F1=1による点2の変位d2=C21は,点2の荷重F2=1による点1の変位d1=C12に等しい」という形で,ベッティやマクスウェルの相反定理により,撓性マトリクスCが対象であることがわかり,その逆行列kもまた対象となることにより証明される.
- どの行の要素の和もゼロになる:剛性マトリクスの行列式の値はゼロとなり,このままでは剛性マトリクスは特異となる.したがって,逆行列は存在せず,剛性方程式として解けない.これは,各行がつり合い式を表していることによるが,系全体が剛体運動をすることが可能であり,変位が定まらないことを意味している.したがって,剛体運動を防ぐ変位の拘束条件(境界条件)を与えることにより,解を求めることができる.
- 主体各要素はすべて正である:これは,正の節点力に対して,正の節点変位を生じることを意味しており,当然である.
これらの性質は,コンピュータによる数値計算などにおいて途中の計算のチェックに利用するとよい.
