4.8.1 残留応力
残留応力が存在すると,外力の作用を受けたときに柱断面内に生じる応力分布は,この外力によって生じる一様分布する応力と残留応力との和で表され,たとえ中心圧縮を受ける柱であってもその応力分布は一様でなくなる.圧縮応力の最大値が降伏応力に達するとこの部分で降伏が始まり,外力の増加とともにこの降伏領域が広がっていく.残留応力が柱の座屈強度に影響を及ぼすのは,応力分布が一様でなくなることと,部分的に降伏することによって断面の剛度が低下することの2つの原因による.前者はねじり座屈およびねじりと曲げとの連成座屈のみに影響するのに対し,後者は曲げおよびねじりのどちらの座屈にも影響する.
4.8.2 曲げ座屈
等断面柱の曲げ座屈荷重は式(4.1)で求められる.柱断面内に残留応力が存在する場合でも,その残留応力の分布が柱の長さ方向に変化することがなく,部分降伏による曲げ剛性の変化が柱の長さ方向に一様であれば,座屈荷重は式(4.1)の曲げ剛性EIを,部分降伏を起こした状態での曲げ剛性で置き換えることによって求められる.
接線係数理論によれば非弾性領域で座屈する場合,縦弾性係数を接線弾性係数で置き換えればよい.したがって,非弾性領域で座屈する場合の曲げ剛性は,

と表される.残留応力を含む柱では内部応力分布が均一でないため,接線弾性係数の値は断面内で一定でなくなる.このために式(4.74)の積分を解析的に行うことは一般の材料,断面では困難である.鋼材の場合には応力-ひずみ関係は完全弾塑性体に近く,完全弾塑性体と仮定すると接線弾性係数値はその部分が降伏しているか,いないかによって0,もしくはEとなる.したがって,部分降伏した領域を除き弾性部分のみを有効と考えてよく,曲げ剛性は,

と表される.ここに,Ieは弾性部分のみを考えた断面の断面主軸に関する断面二次モーメントである.式(4.75)を式(4.1)のEIと入れ換えることによって,残留応力が存在し,部分降伏した柱の座屈強度は次式で求められる.

式(4.76)を断面の降伏荷重で無次元化し,さらに正視化することを考慮して書き直すと,

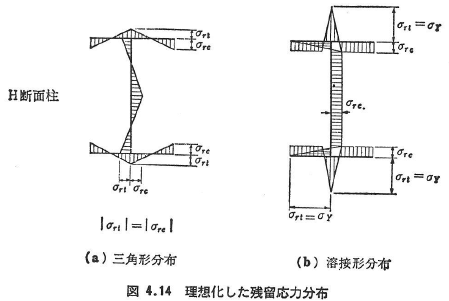
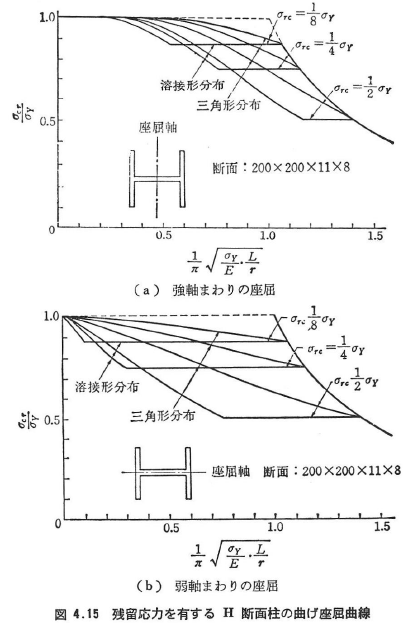
式(4.77)を用いて,図4.14に示す理想化した残留応力を有するH形断面柱について数値計算した結果を図4.15に示す.
4.8.3 ねじりおよび曲げとねじりの連成座屈
曲げ座屈の場合には,残留応力が存在し断面内の応力分布が均一でなくなっても,断面内に部分降伏が生じない限り座屈荷重に影響しないのに対し,ねじり座屈の場合には弾性状態でも応力分布が異なることによって座屈荷重も異なる.一般的には断面のせん断中心から離れた所に圧縮応力が分布するような残留応力が存在すると座屈荷重は減少し,反対に同じところに引張応力が分布するときには座屈荷重は増大する.
二軸対称断面の柱の二軸対称の残留応力が存在する場合の座屈条件式は次式で表される.

ここに,aはせん断中心から断面内の面積要素dAに至る距離を表す.曲げねじり剛性は,

ここに,Cωeは弾性部分のみによる曲げねじり定数である.ねじり剛性Cについても弾性部分のみを考慮して求められる値を用いられることが多い.式(4.78)の条件が満たされたときの座屈荷重は次式で求められる.

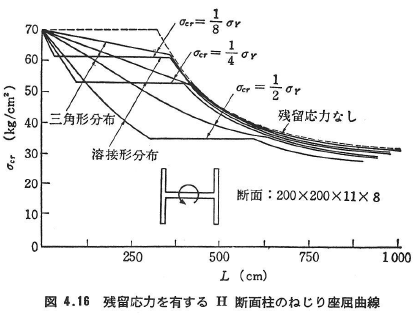
式(4.78),(4.80)を用いて図4.14に示す理想化した残留応力を有するH形断面柱について数値計算した結果を図4.16に示す.