座標
直行直線座標(x,y,z),(x1,x2,x3)
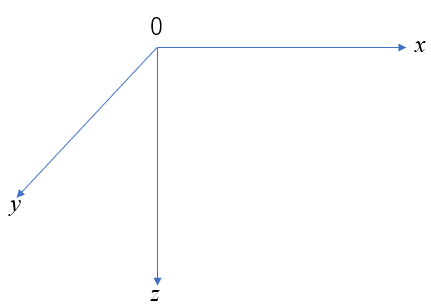
右手系,二次元座標で表示する場合,原則として表示しない他の一軸は紙面奥から手前に向かうものとする.
骨組直線部材では断面をyz軸,部材軸をx軸とする.平面内の骨組では,部材軸xに直角にz軸を用いる.平板では,平面内にxy軸,面外にz軸をとる.他の構造物については必ずしも統一した座標を用いていないので注意のこと.
平面直行曲線座標(ε,η)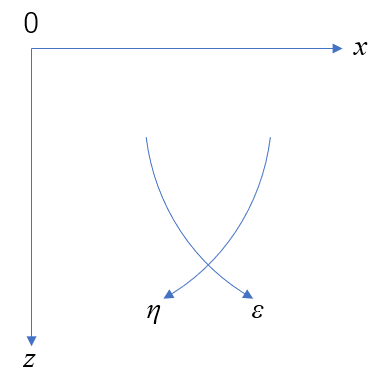
円筒座標(r,θ,xまたはy,z)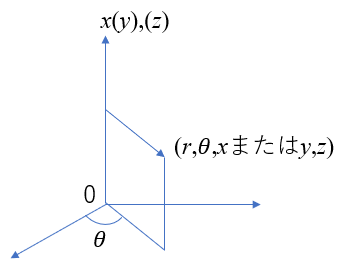
球座標(r,θ,φ)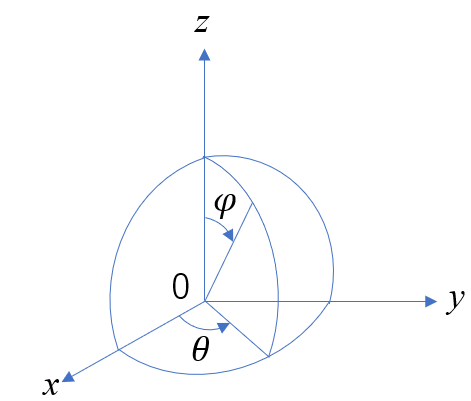
記号
記号のうち,ここで定義されていないものは各章で定めている.添字は必要に応じて使用している.ただし添字のうち以下のものは原則として次の意味を持つ.
| x,y,z | 座標軸 | (例)(σx,σy,σz) | a | 許 容 | (例)(σa) |
| cr | 限 界 | (Pcr) | l | 引 張 | (σta) |
| st | 静 的 | (σst) | c | 圧 縮 | (σca) |
| dy | 動 的 | (σdy) | u | 終 局 | (σu) |
| 0 | 初 期 | (σ0) | T | ねじり | (MT) |
| n | 法 線 | (σn) | p | 極 | (Ip) |
| – | 平 均 | Y | 降 伏 | (σY) |
1.ベクトル
| i,j,k | 単位(基底)ベクトル |
| r(x,y,z) r(r,θ,z),r(r,θ,φ) | 位置ベクトル |
| u(u,v,ω) u(ur,uθ,uz),u(ur,uθ,uφ) | 変位ベクトル |
| P(Px,Py,Pz),F(Fx,Fy,Fz) S(Sx,Sy,Sz) | 力のベクトル |
| M(Mx,My,Mz) | モーメントのベクトル |
2.ベクトルの表示
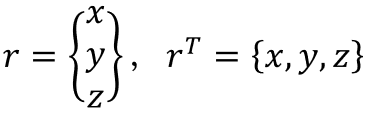
3.行列表示
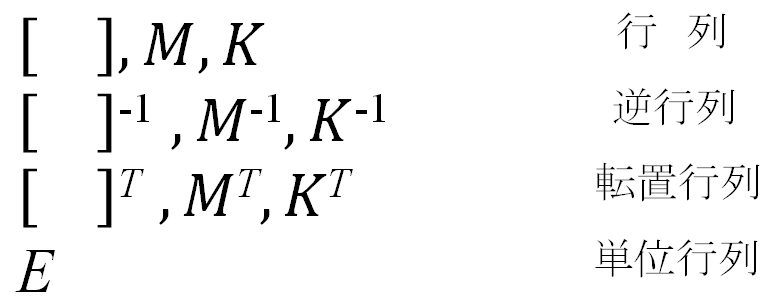
4.行列式

5.応力テンソル
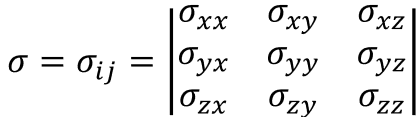
6.ひずみテンソル
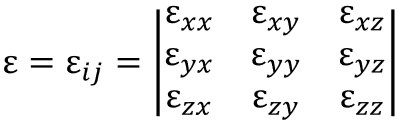
7.力・荷重・モーメント
| N,T,Q,V,M,MT | 断面力 |
| X,Y,Z | 物体力 |
| P | 集中荷重 |
| PE | オイラー荷重 |
| p,q,m,t | 軸直角方向分布荷重, 曲げ及びねじり分布荷重 |
| V,H,R | 反力 |
| p | 圧力 |
| W | 重量 |
| ɤ | 単位体積重量 |
8.応力とひずみ
| σ | (垂)直応力(度) |
| τ | せん断応力(度) |
| ε | (垂)直ひずみ |
| ɤ | せん断ひずみ |
| σ1,σ2,σ3 | 主応力 |
| ε1,ε2,ε3 | 主ひずみ |
| σY | 降伏点,降伏応力 |
| σeq | 相当応力 |
| σm | 平均応力 |
| σcr | 限界応力 |
| σE | オイラー座屈応力 |
| φ,Ø,F | 応力関数 |
9.たわみと変位(一般的な変位表示は1.ベクトルの項参照)
| v,ω,δ | はりのたわみ |
| ω | 板のたわみ |
| θ | はりのたわみ角 |
| φ | はりのねじり角 |
| r | 曲率半径 |
| k | 曲率 |
| ψ,ω | そり関数 |
10.断面の諸量
| G | 断面一次モーメント |
| I | 断面二次モーメント |
| Ip | 断面極二次モーメント |
| W | 断面係数 |
| Z | 塑性断面係数 |
| r | 回転半径 |
| λ | 細長比 |
| J | ねじり定数 |
| Iω,Cω | 曲げねじり定数(そりねじり定数) |
| D[=Eh8/12(1-ν2)] | 板の曲げ剛性(等方性板) |
| t,h | 板厚 |
| a,b | 板または断面の幅 |
| h,d,b | 板または断面の高さ |
| l,Δl | 長さおよび長さの変化 |
| V | 体積 |
| d,D | 直径 |
| r,R | 半径 |
| A,dA | 横断面の面積および微小面積 |
| S,dS | 境界面の面積および微小面積 |
| k | せん断形状係数 |
| k | 座屈係数,ばね定数 |
11.材料の定数
| E | 縦断性係数 |
| G | せん断弾性係数 |
| K | 体積弾性係数 |
| ν | ポアソン比 |
| m | ポアソン数 |
| α | 線膨張系数 |
| αa | 面積膨張係数 |
| αv | 体積膨張係数 |
| ρ | 密度 |
| m | 単位長さ,あるいは 単位体積あたりの質量 |
| M | 集中質量 |
12.仕事量・エネルギー
| W,W* | 仕事および補仕事 |
| T | 運動エネルギー |
| U,U* | ひずみエネルギーおよび 補ひずみエネルギー |
| H,H* | ポテンシャルエネルギーおよび 補ポテンシャルエネルギー |
13.その他
| t,T,Δt,ΔT,dt,dT | 温度および温度変化 |
| g | 重力の加速度 |
| t,Δt,dt | 時間および時間の変化 |
| τ | 遅れ時間 |
| n | 個数,次数,回数 |
| λ | 波長 |
| k | ばね定数 |
| v | 速度 |
| Q(t) | 一般外力 |
| 加速度 | |
| ω,p | 角(円)振動数 |
| n,f | 振動数 |
14.骨組部材の曲げモーメントとせん断力の正負
曲げモーメントとせん断力の添字,正負は,部材xと断面の外向き法線ベクトルが一致する断面(正の断面)でベクトルの成分となるよう定める.ただし,平面内の骨組では添字を省く.
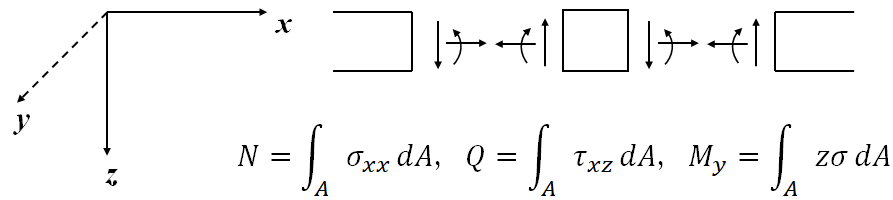
15.曲げモーメントの図示の方法
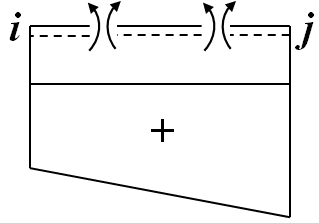
正の曲げモーメント
・・・側に引張応力が生じる曲げモーメントを正とし,引張応力の生じる側に曲げモーメント図を描く.
16.支持条件,節点等の記号
| 固定端 | |
 | ヒンジ端 |
| ヒンジ | |
| 固定ヒンジ支点 | |
| 可動ヒンジ支点 | |
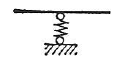 | 弾性沈下支点 (ばね支点) |
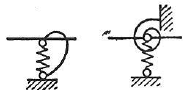 | 弾性沈下回転支点 |
| ねじり回転拘束 | |
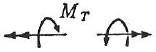 | ねじりモーメント |
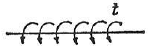 | ねじり分布荷重 |
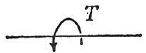 | ねじり集中荷重 |
 | 曲げモーメント |
