malme.app

記事一覧に戻る

構成式

2024年05月17日
構成式

1.4.1　式と用語の定義

構成関係式　　物質（材料）の特性を応力，ひずみならびにそれらの時間的変化などを用いて表現した式を構成関係式，あるいは構成式という．
　以下に，構成式を表現するもに関連する基本的用語を定義する．

  • 荷重-変形図
    ある材料で試験片を作り，これを材料試験機に取り付けて荷重をかけ静かに増加する．この時生ずる変形量とこれに相当する荷重の大きさを直行直線座標上に描いた線図．
  • 公称応力度
    試験片に加わる軸方向荷重Pを，その方向と直交する元の断面積Aで除して得られる値．
  • 真応力度
    試験片に加わる軸方向荷重Pを，その段階でのその方向と直交する真の断面積A’で除して得られる値．
  • 公称ひずみ
    試験片の平行部分上に標点距離l0をとり，変形後の距離lを測定して得られる変形量Δl=l–l0を変形前の標点距離l0で除して得られる値．
  • 対数ひずみ
    刻々の伸び増分dl/lを積分して得られる値．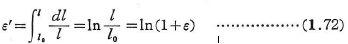
  • 応力-ひずみ図
    応力とそれに対応するひずみとを直行直線座標にとって描いた線図（図1,21）．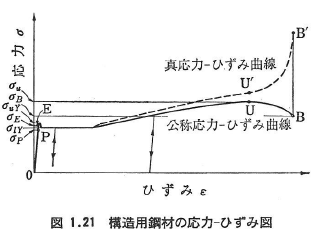
  • 比例限度
    応力とそれによって生じるひずみとの間に正比例の関係が成立する最大限の応力，すなわち，図1.21の応力-ひずみ図の直線から曲線に移る境界の点Pに相当する公称応力σP=PP/A．
  • 弾性限度
    応力によって生じたひずみが応力を取り去ると同時に消失するとき，その材料は完全弾性を示すという．完全弾性を示す最大限の点Eに相当する公称応力σE=PE/A．
  • 上降伏点・下降伏点
    応力が弾性限度を超えて増加しσuY点に達すると試験片のある部分に急激なすべり現象が現れ，荷重はσuY点からσlY点まで急激に降下する（図1.21）．このσuY点に相当する公称応力σuy=Puy/Aを上降伏点，σlY点に相当する公称応力σlY=PlY/Aを下降伏点，あるいは単に降伏点という．明瞭な降伏点を持たない材料については，残留ひずみが0.2%となる応力度（図1.22）．
  • 降伏ひずみ
    降伏応力σYに相当するひずみ．

    ここに，E：縦弾性係数．
  • 引張強さ・圧縮強さ
    引張試験または圧縮試験において材料が耐えられる最大応力，応力-ひずみ曲線の最高点に相当する応力．
  • 極限強さ
    引張試験において材料が破断するときの応力度．
  • 縦弾性係数
    材料の比例限度内において，単軸応力状態で与えられる引張応力，または圧縮応力の変化σと，これに相当する引張ひずみまたは圧縮ひずみの変化εとの比．

    等方弾性体の場合は，これをヤング率（Young’s modulus）ともよぶ．
  • 割線弾性係数・接戦弾性係数
    応力ひずみ曲線上の点Pと原点Oとを結ぶ直線の勾配

    を割線弾性係数といい，点Pの接線勾配，

    を接線弾性係数という（図1.23）．
  • せん断弾性係数
    比例限度以下において，単純せん断応力状態で与えられるせん断応力の変化τと，これに相当するせん断ひずみの変化γとの比．
  • ポアソン比
    弾性体が，一軸方向の荷重を受けるとき，荷重軸方向に縦ひずみε=Δl/lが生ずるとともに，これと直交する方向に横のひずみε1=Δd/dが生ずる．この横方向のひずみε1と縦軸方向のひずみεとの比の絶対値をポアソン比（Poisson’s ratio）という．これは材料の種類によって定まる定数である．
  • ポアソン数
    ポアソン比の逆数
  • 線膨張係数

    ただし，l0：0℃における長さ．T1℃とT2℃の間の平均値は，

    ここに，l1，l2：T1℃，T2℃における長さ．
  • 体積膨張率

    ただし，V0：0℃における体積，V：T℃における体積．T1℃とT2℃の間の平均値は，
  • 体積ひずみ
    物体がその表面に作用する応力によって生ずる体積変化率ΔVと元の体積Vとの比．
  • 体積弾性係数
    弾性体の全表面に働く一様な応力（例えば水圧）の変化Pとそれによって生ずる体積ひずみεvとの比．
  • 塑性変形
    材料に弾性限度を超えて荷重を加えると，荷重を除いても変形が元にもどらないような永久変形を起こす．この変形を塑性変形という．
  • ひずみ硬化
    試験片に引張荷重を加え，材料を初期降伏（初めて降伏すること）ひずみを超えて変形させるとき，新しい降伏応力が最初の降伏応力より上昇するような現象．軟鋼，銅，アルミニウムなどの延性材料に見られる（図1.24）．
  • バウシンガー効果
    試験片に引張荷重を加えたときの降伏応力σYc‘が最初の圧縮降伏応力σYcより減少する現象（図1.25）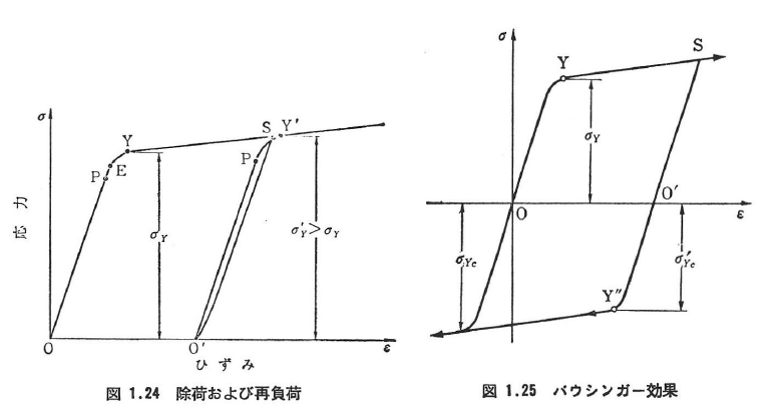
  • 応力増分・ひずみ増分
    ある時刻における材料内の任意の点（x，y，z）の応力状態（σxx，σyy，σzz，σxy，σyz，σzx）およびひずみ状態（εxx，εyy，εzz，εxy，εyz，εzx）が微小時間の後にそれぞれ（dσxx，dσyy，dσzz，dσxy，dσyz，dσzx）および（dεxx，dεyy，dεzz，dεxy，dεyz，dεzx）だけ変化したとするとき，この応力およびひずみ微小変化．
  • ひずみの弾性成分・塑性成分
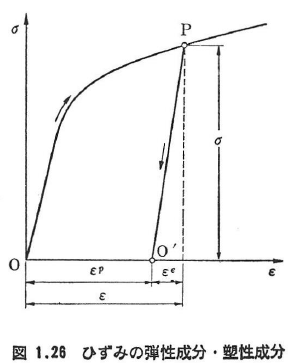
    応力-ひずみ図の弾性限度を超えた点Pより除荷するとき，回復可能なひずみを点Pに相当する全ひずみεの弾性成分εe，残留する永久的なひずみを塑性成分εpという（図1.26）．

    同様に，ひずみ増分dεも弾性ひずみ増分dεeと塑性ひずみ増分dεPに分けることができる．

  • クリープ
    一定応力下で時間経過とともに生じる進行性変形．ひずみの時間変化率（増分）などが示量となる．
  • 応力緩和
    一定に保持したひずみ（変形）の下で時間経過とともに生じる進行性応力変化．応力の時間変化率（増分）などが示量となる．

1.4.2　構成関係のモデル化

構成関係を分類すると次のようになる．

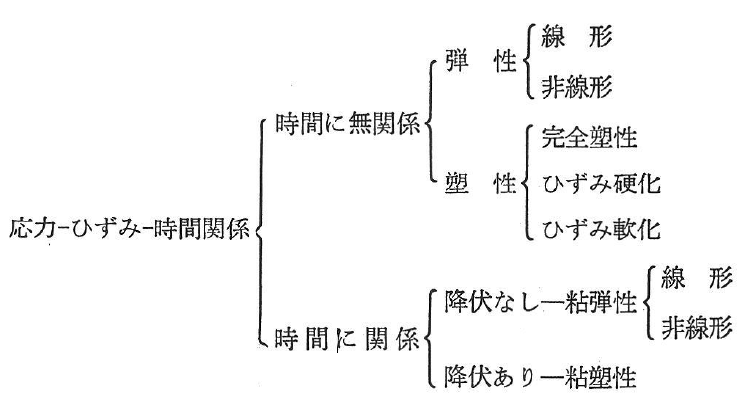
代表的な構成関係のモデルを図1.27に示す．参考のため機械要素による特性表示も図1.28に示す．

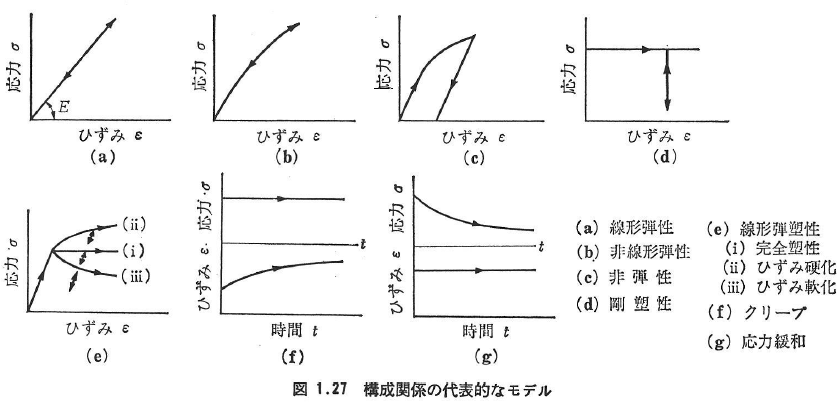
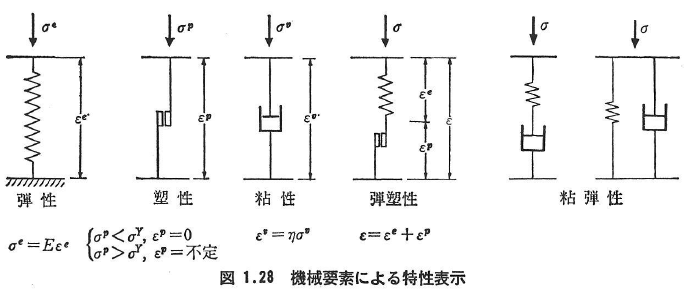
1.4.3　弾性体

（a）Green弾性体（超弾性体）

　弾性ポテンシャルが存在するような弾性体をGreen弾性体または超弾性体という．弾性ポテンシャルρU（ρは密度）をひずみεijのべき級数で表す．三次以上の項を無視し，自然状態（ひずみもおうりょくも0）を基準とすると，

という二次形式で表される．ここに，Aijklは係数である．
　このポテンシャルより，応力は

と求まる．これを一般化フック（Hooke）の法則という．
　式（1.89）は，応力とひずみの線形関係を示している．応力とひずみの対称性およびポテンシャルの存在から，Aijkl=Ajikl=Aijlk=Aklijとなり，Aijklの独立な成分の数は21個となる．

（b）Cauchy弾性体

　弾性ポテンシャルの存在を仮定せずに，単に応力とひずみが1対1に対応する構成式をもつ材料は，Cauchy弾性体とよばれる．この場合も式（1.89）と同様な関係が導かれる．応力とひずみの対称性および熱力学的考察から，Aijkl=Ajikl=Aijlk=Aklijが要請され，Aijklの独立な成分の数は21個となる．

（c）亜弾性体

　応力状態がひずみおよびひずみの履歴の関数として定義される弾性体．増分形では次のように与えられる．

Fij（dεkl，σmn）は弾性応答関数である．

（d）直交異方性と等方弾性体

　式（1.89）の表示を，対称性を考慮して行列表示すると次の関係を得る．

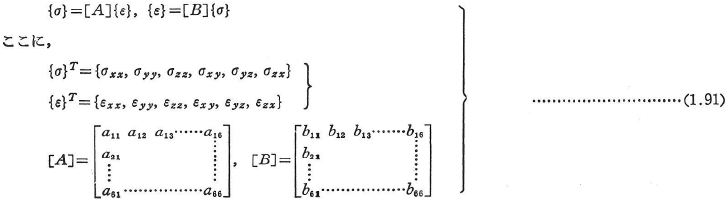
  1. 直交異方性の場合　　異方性の主軸を座標軸方向に一致させてとると次のようになる．

    ［B］についても同様な形を得る．
  2. 等方性の場合　　ヤング率E，ポアソン比ν，せん断弾性係数Gを用いると，式（1.91）のうち0でない係数は次のようになる．

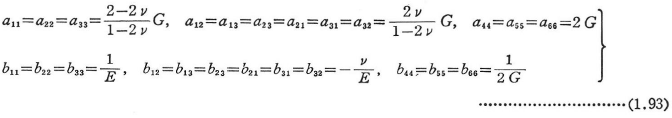
    式（1.89）は次のようにも書ける．
  3. 熱弾性体の場合
    温度上昇ΔTに伴うひずみは，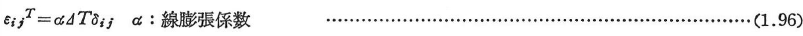

    で与えられる．応力と温度上昇が同時に加えられる場合には，全ひずみは，それぞれによるものの和で与えられると仮定すると，次のように与えられる．

1.4.4　線形粘弾性体

（a）積分表現

　応力σij(x，t)，ひずみεij(x，t)の関係は次のような合成積分で与えられる．

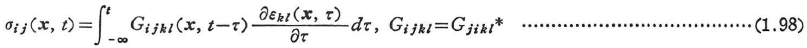
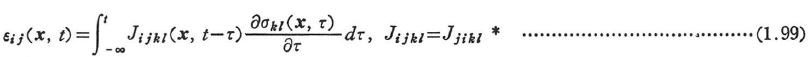
ここに，，Gijklは応力緩和関数，Jijklはクリープ関数とよばれる．
t＜0ではσij＝εij＝0とし，t=0で運動が始まったとすると，式（1.98）は次のように書ける．

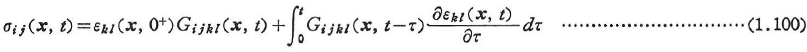
合成積分I(t)を

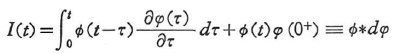
と略記すると，式（1.98），（1.99）は次のように書ける．

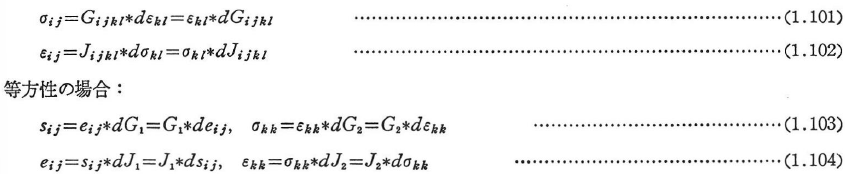
G1(J1)，G2(J2)は，それぞれせん断応力緩和（クリープ）関数，体積応力緩和（クリープ）関数とよばれる．

（b）微分表現

微分形では，次のように与えられる．

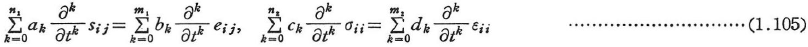
ak，bk，ck，dkは材料定数である．

（c）ラプラス（Laplace）変換と弾性-粘弾性対応原理

　式（1.103），（1.104）のLaplace変換

をとると，

を得る．一方，弾性体の構成式，式（1.95）のLaplace変換は，

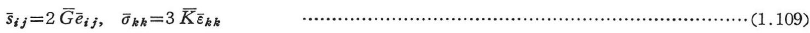
となる．両者を比較して，次の関係を得る．

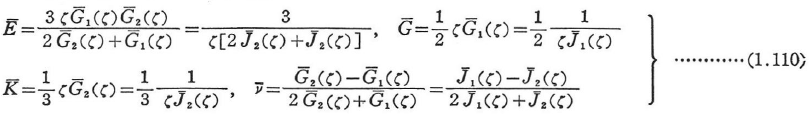
一方，つり合い式，式（1.17）とひずみと変形の関係，式（1.52）のLaplace変換は次のようになる．

　境界条件もLaplace変換をとって表すことにすると，線形粘弾性体の境界値問題は，Laplace変換を取った像空間で，式（1.111），（1.112）と（1.107）または（1.108）を境界条件のもとで解くことに帰着する．この関係を線形弾性体の場合と比較すると，式（1.107），（1.108）を除けば，弾性の場合の変量の上に形式的にバーを付けた形となっていることがわかる．すなわち，線形弾性体の場合とは構成式だけが異なっている．
　一方，式（1.107），（1.108）と式（1.109）を比較すると，式（1.110）のように，弾性体のと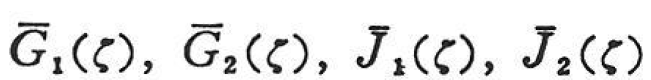の関係が与えられているので，粘弾性体の境界値問題を解く代わりに，Laplace変換した弾性解を用い，その係数などを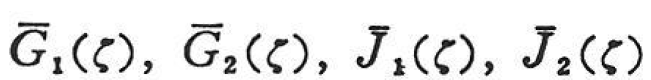，で置き換えるだけで，Laplace像空間での粘弾性解が求められることになる．これを弾性-粘弾性の対応原理という．粘弾性体の境界値問題の解は，この像空間での解を逆変換して求められる．この場合，解の一意性も保証される．
　したがって，線形粘弾性体の境界値問題の解は，対応する弾性体の境界値問題の解が得られておれば必ず求められる．
　なお，境界条件が時間とともに変化するような境界値問題に対しては，この対応原理は適用できない．

1.4.5　弾塑性体

（a）降伏曲面

　自然状態で応力が0である物体に図1.27(e)に示すように応力を増加させたとき，最初に達する降伏を初期降伏，その応力を初期降伏応力という．さらに負荷，除荷，負荷のサイクルによって生じる降伏を逐次降伏あるいは後続降伏という．
　一般的な組合せ応力の下でも降伏が生じる．それは一軸応力での結果から類推して，（主）応力空間（（主）応力を座標軸とする空間）内の曲面で表示できる．これを降伏曲面という．
　降伏曲面は一般的には，σijを座標軸とする六次元空間（σij=σjiを考慮する），あるいは主応力σ1，σ2，σ3を座標軸とする三次元空間内の曲面として表される．一般的に，その曲面は凸曲面である（降伏曲面の凸性）．
　弾性-完全塑性体モデルに対しては，降伏曲面は応力空間内に固定されており，この曲面の内側の応力状態はすべて弾性的挙動を示し，この曲面上で表される応力状態になると変形が際限なく進行することを意味している．なお，曲面の外部で表されているような応力状態は実現されない．
　ひずみ硬化するモデルでは，初期降伏曲面は応力空間内に固定されているが，後続の降伏に応じてこの曲面の一部，あるいは全部が移動ないし変形することになるわけである．

降伏曲面の例

  1. フォン・ミーゼス（von Mises）：主応力空間内で静水圧軸（σ1=σ2=σ3）を中心軸とする円柱の表面
  2. トレスカ（Tresca）：主応力空間内で静水圧軸を中心軸とする正六角柱の表面
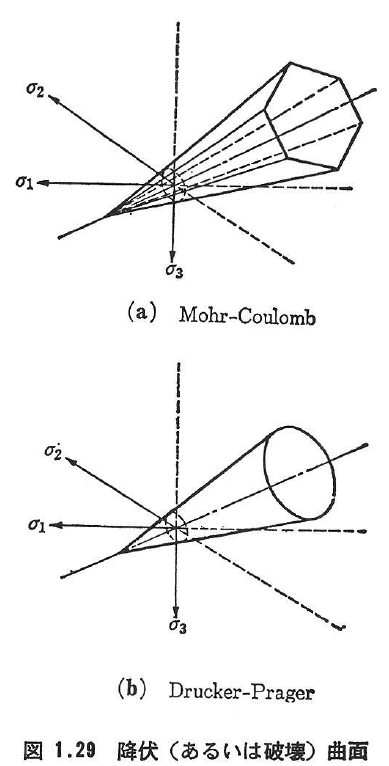
  3. モールークローン（Mohr-Coulomb）：主応力空間内で静水圧軸を中心軸とする六角錐（正三角よりやや膨らんだ六角錐）の表面，三軸等引張応力状態が頂点となる（図1.29(a)）．
  4. ドラッカー-プラーガー（Drucker-Prager）：主応力空間内で静水圧軸を中心軸とする円錐表面，三軸等引張応力状態が頂点となる．（図1.29(b)）などが考えられる．

（b）降伏関数

　降伏曲面を応力σij，または主応力σiの関数として表す関係式

を降伏関数という．
　降伏関数に関しては，

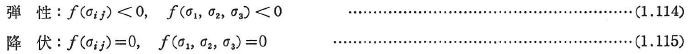
である．f(σij)>0，f(σ1，σ2，σ3)>0は実現されない．

　降伏関数の例：前述の例を示す．

  1. von Mises：
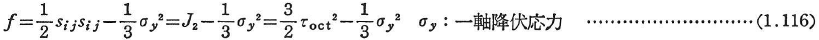
  2. Tresca：
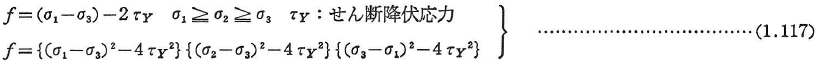
  3. Mohr-Coulomb：
  4. Drucker-Prager：

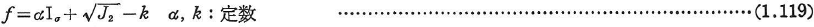
（c）除荷と負荷

  1. 塑性ひずみ
    弾塑性体のひずみεijは，弾性ひずみεijeと塑性ひずみεijpの和で表される．したがって，その増分は，

    となる．
  2. Druckerの公準
    Druckerの安定な材料の公準：「つり合い状態にある物体（材料）に外部から準静的に荷重を加えた後，これを除荷するという過程を考えると，この荷重によってなされる仕事は正であり，負荷除荷の1サイクルによる仕事の緩和が０または正であるならば，この物体（材料）は安定である」．これは次のように表現される．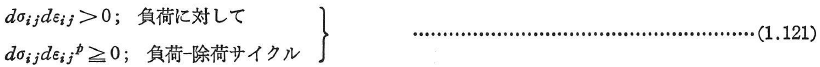

    完全塑性体に対しては，等号が成立する．
    降伏関数を，塑性ひずみεijpや負荷の履歴に依存するパラメーターkを用いて

    と表すと，”負荷”，”除荷”，”中立負荷”の基準は次のように表される．
  3. 降伏曲面の凸性，塑性ひずみ増分の法線則と随伴流れ則
    　式（1.121）によれば塑性ひずみ増分ベクトルdεijpは，応力増分ベクトルdσijと鋭角をなすことが要求される．すべてのdσijに対してこの条件を満たすためには，dεijpは降伏曲面に垂直でなければならないこと（塑性ひずみ増分の法線則）がわかる．
    　また，このような降伏曲面に垂直な塑性ひずみベクトルが，式（1.121）を常に満たすためには，降伏曲面は凸でなければならないこと（降伏曲面の凸性）もわかる．
    　なめらかな降伏曲面上では，塑性ひずみ増分は

    と表現される．これを随伴流れ則という．
    　式（1.122）で表される降伏関数を用いると，負荷過程では応力点は常に降伏曲面上にあるから，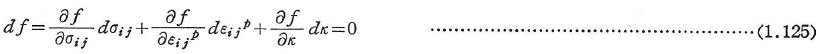

    となる（Pragerの適応条件）．一方，kをひずみ履歴の関数，k(εijp)とすると，式（1.125）より，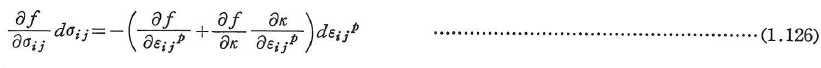

    を得る．
    　したがって，式（1.124）は，次のように書き換えられる．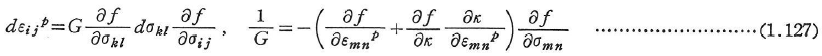

    　完全塑性材料では，降伏曲面はf(σij)=0で表されるので，式（1.124）のλは未定である．
    　なお，式（1.124）をみると，降伏関数fは塑性ひずみ増分を導出するためのポテンシャルであるので，このfをしばしば塑性ポテンシャルとよんでいる．したがって，上記の場合，塑性ポテンシャル面は降伏曲面に一致する．
  4. 線形弾性-塑性体の構成式
    　弾塑性体の応力-ひずみ関数式は，式（1.120）に式（1.94），（1.127）を代入して求められる．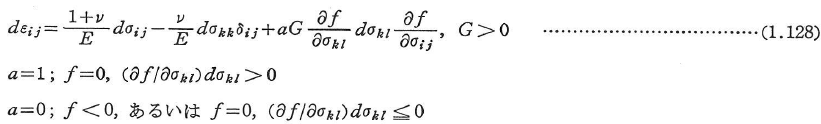

    　完全弾塑性体に関しては次のようになる．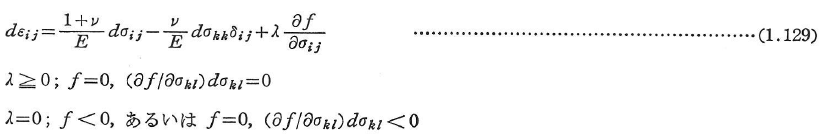

    　なお，摩擦機構が卓越するような材料，例えばMohr-Coulomb条件に従うような材料では，上述の塑性ひずみ増分の法線則は一般には成立しない（非随伴流れ則）といわれており，種々の応力ひずみ関係式が提案されている．
    　弾塑性体が力を受けて変形を生じる際には，降伏条件を拘束条件として満足しつつ，物体内に応力，ひずみあるいは変形が定められることになる．