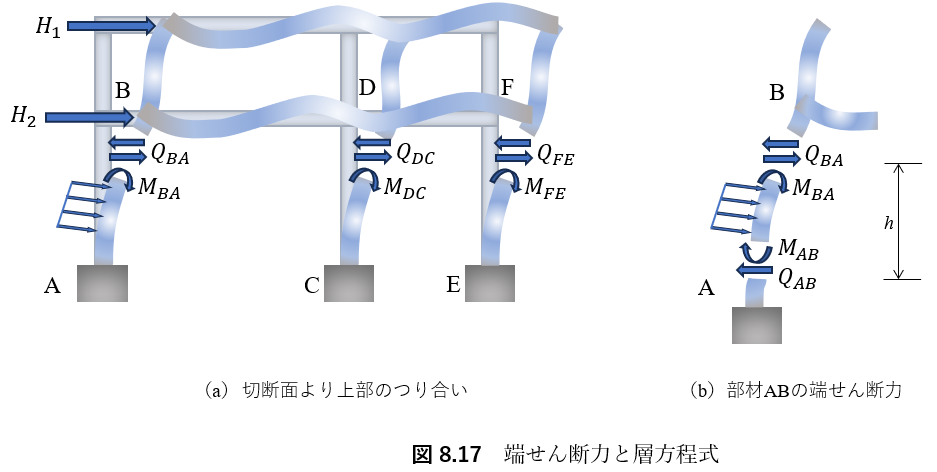
8.8節で述べたように，温度変化や支点沈下によるのではなく，外力によって節点が変位を生じ，それにともなって部材角を生じる場合は，節点方程式だけでは方程式が不足するので，未知の部材角を決定するために，水平方向のせん断力に関するつり合い式を考える．
　図8.17(a)に示すように，水平力を受けて変形した２層２スパンのラーメンについて考える．いま，任意の１層を横切って切断したと考え，切断面の上の部分の水平方向のつり合いを考える．柱の切断面には水平方向のせん断力Q_BA，Q_DC，Q_FEが作用しているはずなので，このせん断力の全柱にわたる合計とせん断面より上の部分に作用する外力H₁，H₂の水平成分の総和Hがつりあう条件として次式を得る．

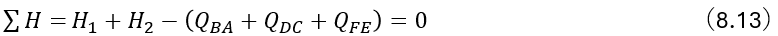
このような層ごとのせん断力のつり合い式をラーメンの層方程式という．一般には，ラーメンの各層にそれぞれ１個の式が成り立ち，未知の部材回転角Rの数と一致して，方程式が解けることになる．

　この部材端ののせん断力Qは，端せん断力とよばれ，端モーメントを求めたあとで，単純ばりの反力として求められる．すなわち，図8.17(b)に示すＡＢ部材について，Ａ端またはＢ端まわりの回転のつり合い式より

となる．ここで，Q_A0，Q_B0は，部材の中間に作用する荷重のみによる反力である．ただし，Q_AB，Q_BA，Q_A0，Q_B0の符号は，遠端を中心にして，部材を時計回りに回転させる向きを正とする．
　部材角が生じる（節点変位が生じる）ラーメンの解法は，8.7節で述べた部材角が生じないラーメンの解法手順と同じであるが，項目③のあとに
　③’式（8.13）の層方程式を作成し，それに端モーメント式を代入して，連立方程式に加える．
を付け加え，①～⑥の各手順の文章中の「たわみ角」の表情を「たわみ角と部材角」に読み変えればよい．

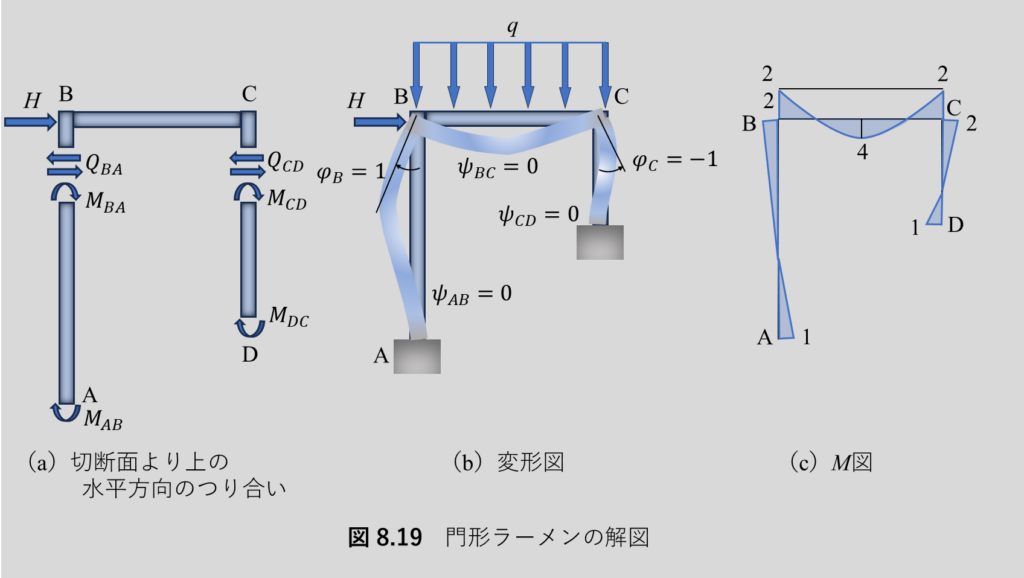
ここで演習問題8.4~8.7を解いてみよう．