Contents
1.2.1 応力
(a)応力ベクトル(表面力)と応力テンソル
- 定義 物体内の1点Oを含む微小面積をΔS,その部分に作用している合力をΔFとする(図1.9).

が存在すれば,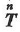 を応力ベクトル,表面力あるいはトラクションとよぶ.ここに,添字nは外向き単位法線ベクトルnで表される面ΔSに作用するベクトルという意味で付けてある.力のつり合いから
を応力ベクトル,表面力あるいはトラクションとよぶ.ここに,添字nは外向き単位法線ベクトルnで表される面ΔSに作用するベクトルという意味で付けてある.力のつり合いから
座標軸に垂直な面に作用する応力ベクトルの各座標軸方向への成分は,応力テンソル,応力度あるいは応力とよばれる.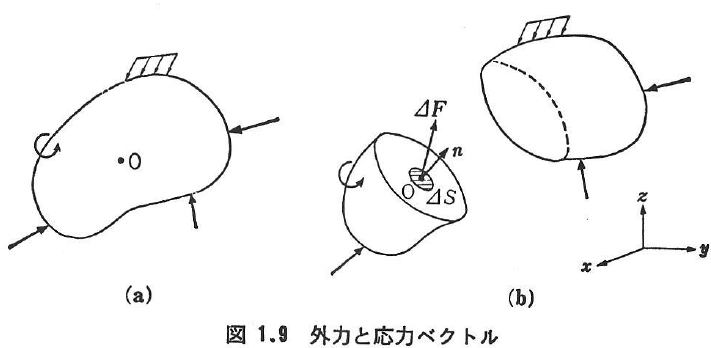
- 応力の表示 応力は一般に2つの添字を用いて書きあらわされる.第一の添字は,応力ベクトルが作用する面の方向を,第二の添字は応力ベクトルの成分の方向を示す(図1.10).行列表示では
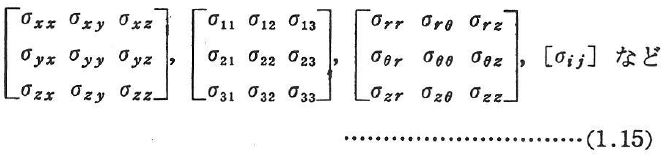
ここに,i,jは直交直線座標(x,y,z)ではx,y,z,(x1,x2,x3)では1,2,3を円柱座標系(r,θ,z)では,r,θ,zなどを表すものとする.成分はσij.なお,σの代わりにτを用いるとか,σxx,σyy,σzzをσx,σy,σzとか,σxy,σxz,σyzなどをτxy,τxz,τyzと書くことも多い.以下,特に断らない限り,直交直線座標で表示する.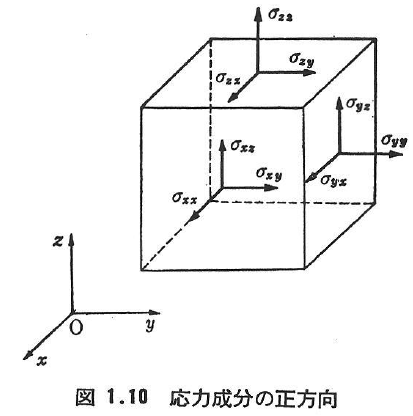
(b)直応力とせん断応力
応力ベクトルの作用する面に垂直方向の成分を直応力,その面内方向の成分をせん断応力という.式(1.15)中,σxx,σyy,σzz;σ11,σ22,σ33とかσrr,σθθ,σzzは直応力を,σxy,σxz,…;σ12,σ13,…;σrθ,σrz,…などはせん断応力を表す.
(c)平面応力状態路一軸応力状態
式(1.15)において,ある方向へのすべての応力成分が0,例えばσzz=σzx=σzy=σxz=σyz=0;σ3i=σi3=0の場合には平面応力状態にあるといい,さらに,2方向成分がすべて0,例えばσxxしか作用しない場合には一軸応力状態にあるという.
(d)表記法
- 座標系(x,y,z)と座標系(x1,x2,x3)を必要に応じて併用する.x↔x1,y↔x2,z↔x3.後者の座標成分をxi(i=1,2,3)と書くこともある.↔は互いに対応することを意味する.
- 上記座標系に応じて,
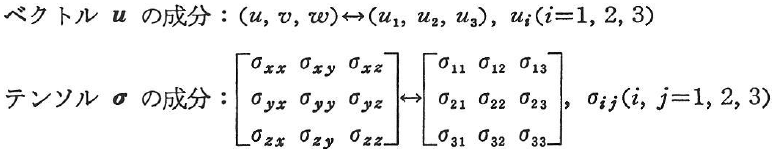
などとする. - 総和規約:座標系(x1,x2,x3)による場合,式とか項において2度現れる添字に関しては,添字の範囲での総和をとるものとする.例えば,
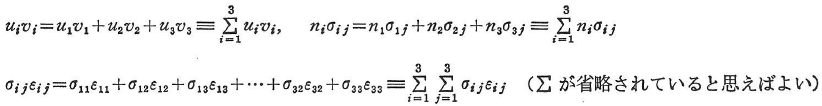
以下添字の範囲は特に断らない限り1,2,3とする.
1.2.2 コーシー(Cauchy)の公式
方向余弦n=(nx,ny,nz)を外向き法線とする表面に作用する表面力![]() の直交直線座標方向の成分,
の直交直線座標方向の成分,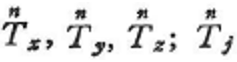 は次のように与えられる.これをCauchyの公式という.
は次のように与えられる.これをCauchyの公式という.
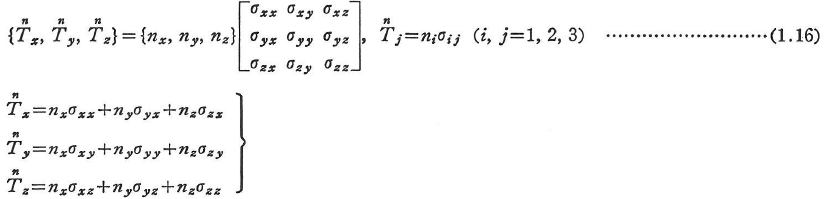
円柱座標系では,上式において,x,y,zをr,θ,zと置き換えるだけでよい.
1.2.3 つり合い式
物体中に微小直方体を考え,そのつり合いを考えると容易に次式を得る(図1.11).
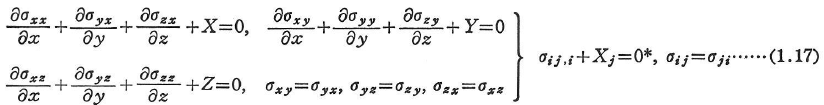
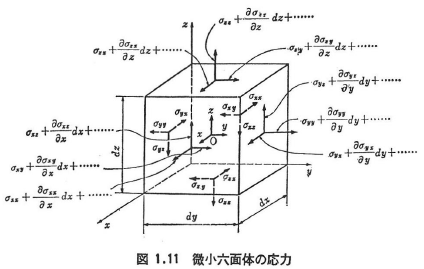
ここに,X,Y,Zは物体力Xのx-,y-,z-軸方向成分である.鉛直座標表示では次のようになる.
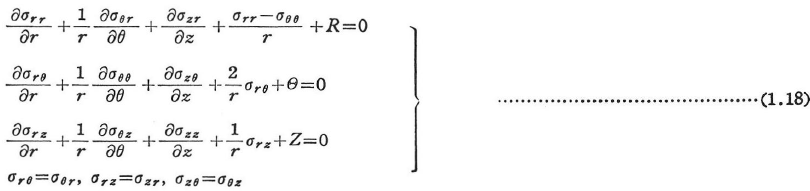
ここに,R,θ,Zは物体力のr,θ,z方向成分である.
1.2.4 座標変換に伴う応力の変換
(a)座標変換
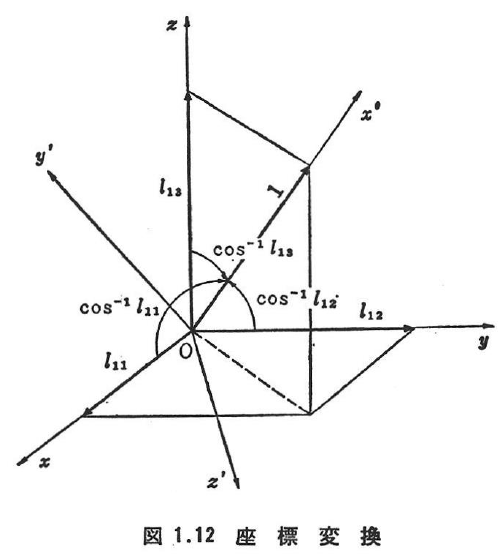
図1.12のように,座標系(x,y,z)から座標系(x’,y‘,z‘)に変換する変換則は次のようになる.
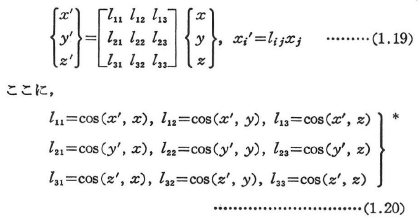
cos(x’,x),cos(x’,y),…は,x’軸とx軸,x’軸とy軸,…との間の角の余弦を意味する.
(b)応力の変換
座標系(x,y,z)での応力成分をσijで表わし,座標系(x’,y‘,z‘)での応力成分をσij‘で表すと,応力の変換は次のように与えられる.
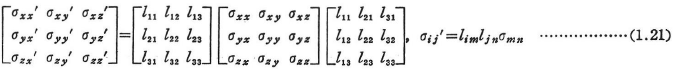
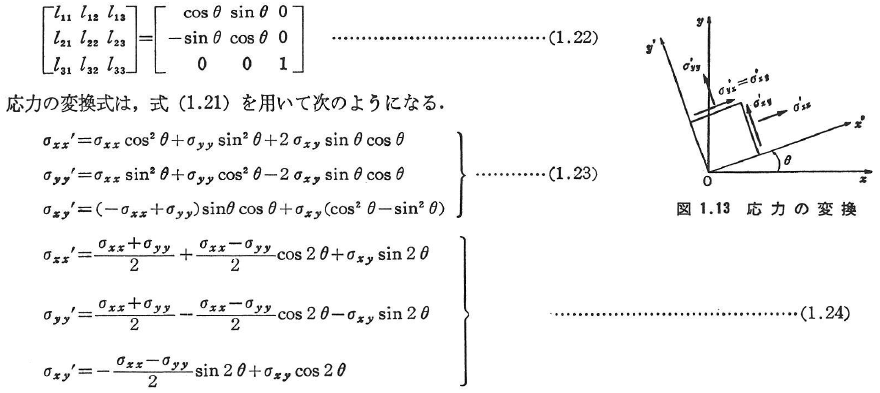
(c)平面応力状態での変換
図1.13に示す二次元座標変換を考えると,式(1.20)の方向余弦は次のようになる.
1.2.5 主応力,偏差応力,八面体応力,相当応力,応力楕円体
(a)主応力と主方向
- 定義 応力ベクトル
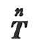 の方向が,それが作用する面の方向nに一致するとき
の方向が,それが作用する面の方向nに一致するとき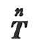 の大きさσ(
の大きさσ(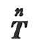 =σn)を主応力,nを主方向とよぶ.
=σn)を主応力,nを主方向とよぶ.
- 主応力 主応力は式(1.25)が解をもつための条件,すなわち次式を解いて求められる.
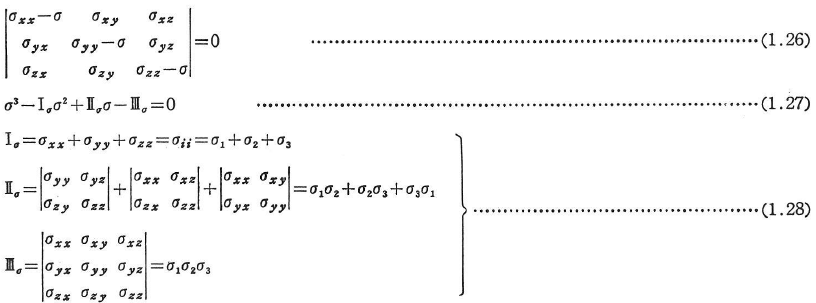
ここに,σ1,σ2,σ3は,式(1.27)の根,すなわち主応力である.Ⅰσ,Ⅱσ,Ⅲσは,それぞれ応力の第1,第2,第3不変量とよばれる.
主応力n,その方向余弦(nx,ny,nz)は,次式を解いて求められる.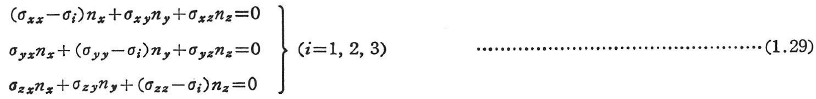
- 主応力はすべて実数値をとる.主方向は,主応力がそれぞれ異なる場合には互いに直交する.また,主応力の2つ以上が一致する場合にも,主方向が互いに直交するように選ぶことができる.
平面応力の場合には,主応力は次のようになる.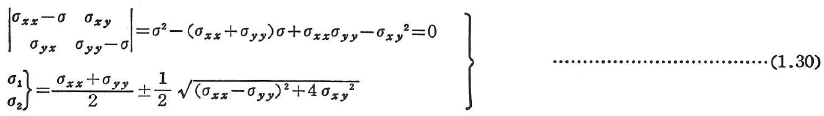
主方向は次式より求められる.
(b)偏差応力
偏差応力は,一般の応力成分から等方応力成分(σm)を差し引いた偏差として定義される.sxx,sxy,…;sijを偏差応力とすると,
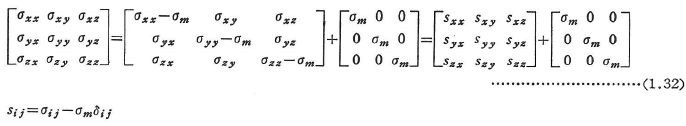
ここに,σmは,等方応力(平均直応力)とよばれる不変量である.
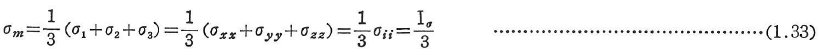
偏差応力に関しても式(1.25)~(1.31)と同様な式が成立する.通常偏差応力の不変量を次のように表す.
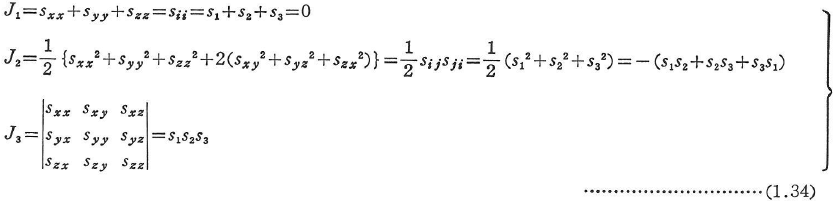
ここに,s1,s2,s3は主偏差応力である.

(c)八面体直応力と八面体せん断応力
主軸方向から等しい傾斜をもつ正八面体に働く応力は八面体応力とよばれる.八面体直応力σoctおよびせん断応力τoctは次のように与えられる.
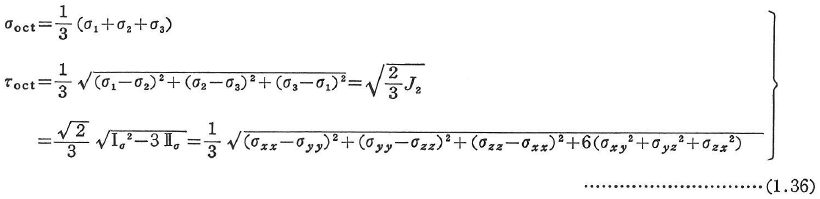
(d)相当応力
応力の成分間の比が一定に保たれたままで増大する場合(比例負荷)には,組合せ応力の効果を一軸応力に換算して考え得ることが多い.このように換算された応力σeqは,相当応力,一般化応力あるいは有効応力とよばれる.例えば,せん断ひずみエネルギー説に従う次式のσeqが用いられることが多い.
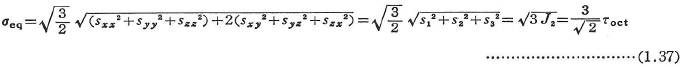
(e)応力楕円体
応力テンソルの主軸(主方向軸)を座標軸x,y,zとすると,次式を得る.

一方nは単位ベクトルであるから,
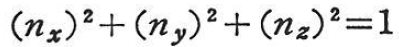
この式に,式(1.38)を代入するとラメ(Lame)の応力楕円体を表す式が得られる.

平面応力状態では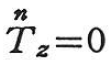 であり,式(1.39)から応力楕円体が求められる.
であり,式(1.39)から応力楕円体が求められる.
1.2.6 モール(Mohr)の応力円
(a)三次元応力状態の場合
主応力をσ1,σ2,σ3(σ1>σ2>σ3),応力ベクトル![]() の直応力成分をσN,せん断応力の成分をσSとすると,
の直応力成分をσN,せん断応力の成分をσSとすると,
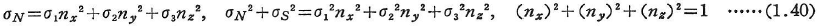
これらの式よりnx,ny,nzを得る.
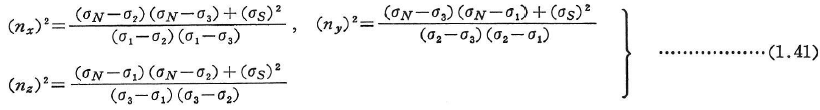
nx,ny,nzをそれぞれ0とした場合のこれらの関係をσNを横軸に,σSを縦軸にとって図示すれば図1.14(a)に示す3個の円が求まる(上半分のみを図示した).これはMohrの円とよばれる.σ1>σ2>σ3,nx2≧0,ny2≧0,nz2≧0であるから,応力状態は図中の円C2で囲まれ,かつ円C1,C2の外側の部分で表される.図1.14(a)のp点の応力(σN,σS)は,図1.14(b)に示す任意点Pの応力ベクトルの成分σN,σSを表している.
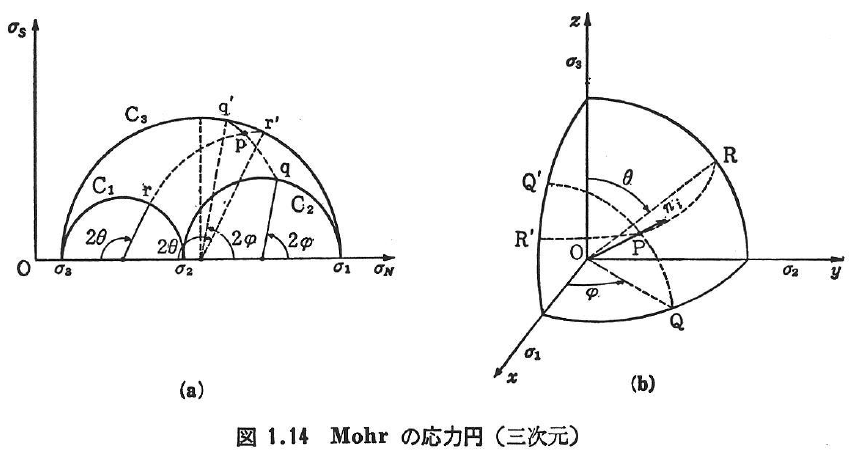
(b)平面応力状態の場合
(a)の特別な場合として,主応力が0という主軸を含む平面上の点の応力状態は,単一のMohrの円で表される.図1.15に平面応力状態およびこれに対応するMohrの応力円を示す.Mohrの応力円では,微小要素上で時計まわり方向に作用するせん断応力を正として描いていることに注意されたい.また,式(1.24)で与えられる応力状態は,Mohrの円で示されるものと一致している.例えば,次式を確かめられたい.
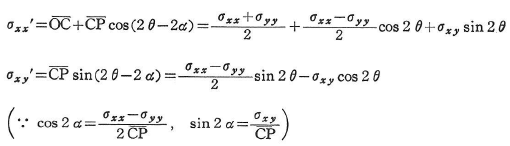
図1.16はMohrの応力円と極,応力状態とその応力の生じる断面(方向)との関係を示した.極は,与えられた既知の応力状態に対応するMohrの応力円上の点を通り,その応力が生じる面の垂直方向と平行に引いた直線がMohrの応力円と交わる点として求められる.極が求められれば,任意方向の断面に働く応力状態は極からその断面の垂直方向に平行に引いた直線とMohrの応力円との交点として求められる.