3.3の線形弾性解析法は,骨組構造物の弾性域内での挙動を解析する,いわゆる設計荷重のもとでの応力や変形を算定することが目的であった.ここでは,延性を有する材料からなる構造物が塑性崩壊するときの崩壊荷重を単純塑性理論に基づく塑性解析により求める.すなわち,塑性解析の目的は,構造物の形式,作用荷重形式および各部材の強度が与えられたときの構造物の抵抗強度いわゆる構造物が崩壊機構を形成するときの荷重を求めることである.換言すれば,既知の断面諸定数をもつ構造形式に対し,ある与えられた作用荷重Pの何倍まで崩壊せずに抵抗し得るか,作用荷重Pに対する崩壊荷重係数αc(崩壊荷重Pc=αcP)を求める問題である.
単純塑性理論に基づく塑性解析では,通常次のような仮定を用いる.
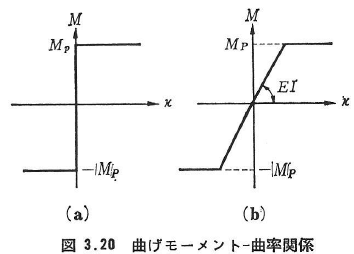
- 材料は剛塑性体であるとし,したがって断面の曲げモーメント(M)と曲率(k)との関係は図3.20(a)のように全塑性モーメント(MP)に達したのちは無制限塑性流れを生ずるものとする.ただし,崩壊時のたわみを求める場合や弾性限を超えた荷重-変形関係を求める場合などの弾塑性解析法では図3.20(b)のような理想弾塑性モデルを用いる.
- よって,塑性ヒンジは断面に集約されるものとし,塑性域の広がりは考慮しない.
- 構造物の変形は微小であり,力のつり合いは変形前の構造系について考える.
- 荷重は各荷重の大きさが一定の比率を保って増加する(比例荷重という).
- 曲げモーメントのみを考慮し,軸力,せん断力の影響は考慮しない.
- 局部座屈および全体座屈などの不安定現象は塑性崩壊に至るまで起こらないものとする.
3.5.1 塑性解析の基本条件
単純塑性理論を用いて崩壊荷重を求めるには,次の3つの基本条件を満足しなければならない.
(a)力のつり合い条件(Equilibrium Condition,Ⓔと略す)
崩壊荷重レベルにおいて,構造物に作用する外力と内力は常につり合いを保っていなければならない.すなわち,静力学的つり合い条件は次式のようになる.

また通常の長方形ラーメンの基本機構には,はり機構,層機構および節点機構の3つがあり,これらに仮想仕事の原理を適用すると,崩壊荷重レベルでの独立なつり合い式が次式のように表される.

ただし,Mj:節点jの作用曲げモーメント,θkj:基本機構kにおける節点jの仮想回転角,ek(=∑Pjδkj):基本機構kにおける仮想外力仕事,Pj:節点jに作用する外荷重,δkj:基本機構kにおける節点jの仮想変位,α:荷重係数,j:節点の数を示す記号,s:全節点数,k:基本機構の数を示す記号,m:基本機構の全数で,次式より求められる.

上式は,各節点に作用しているs個の未知曲げモーメントを求めるために,式(3.94)のようなm個のつり合い式とn個の不静定次数に等しい適合条件式が必要であるという条件(s=m+n)から得られる.
(b)崩壊機構条件(Mechanism Condition,Ⓜと略す)
崩壊荷重レベルにおいて,構造物には十分な数の塑性ヒンジを有する崩壊機構が形成されなければならない.すなわち,ある組み合わせ崩壊機構iの節点jの仮想回転角θjおよび作用荷重のなす外力仕事Eiは,幾何学的制約によりそれぞれ基本機構kにおける節点jの仮想回転角θkjおよび仮想外力仕事ekの一次結合によって次式のように表される.

ただし,tk:基本機構kがある組み合わせ機構に関与する割合を示す係数.
(c)降伏条件(Yield Condition,Ⓨと略す)
崩壊荷重レベルにおいて,構造物内のいかなる節点の曲げモーメントもその点の全塑性モーメントMPjを超えてはならない.
3.5.2 塑性解析の基本定理
簡単な構造物の崩壊荷重は,上記3つの条件を同時に満足するように容易に決定されるが,構造物が複雑になると崩壊荷重を直接求めることが困難となる.そこで次のような定理がよく用いられる.
(a)静的定理または下界定理
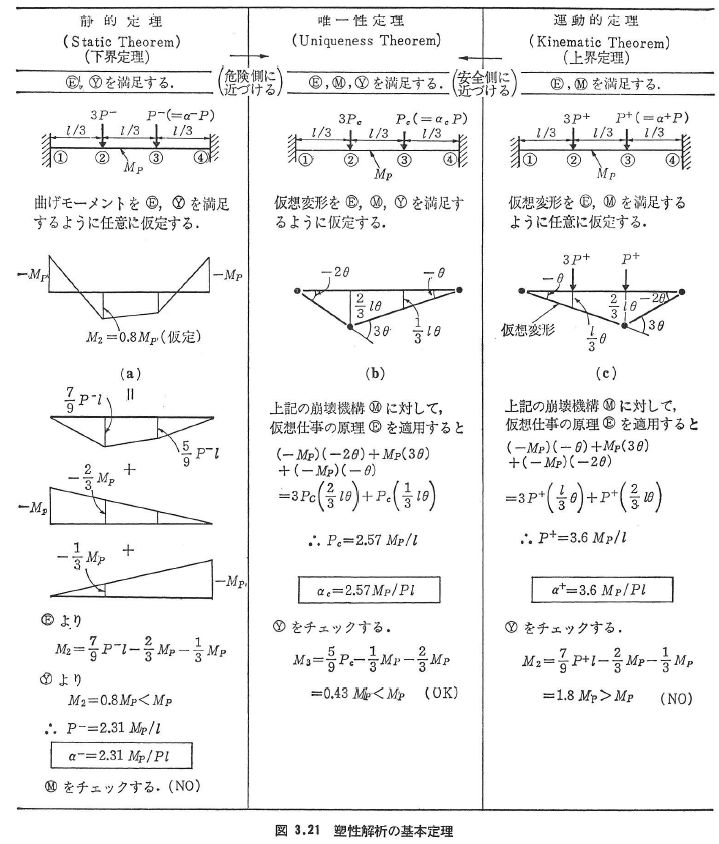
ⒺとⓎを満足するような静的許容応力状態(安全側の応力分布,図3.21(a)参照)の中で得られる荷重P–は真の崩壊荷重Pcより常に低いか等しい(P–≦PcまたはPc=maxP–).また真の崩壊荷重係数αcは静的許容荷重係数α–のうちの最大値をとる(α–≦αcまたはαc=maxα–).
(b)運動定理または上界定理
ⒺとⓂを満足するような運動的許容変形状態(危険側の仮想変形,図3.21(c)参照)の中で得られる荷重P+は真の崩壊荷重Pcより常に高いか等しい(P+≦PcまたはPc=minP+).また真の崩壊荷重係数αcは運動的許容荷重係数α+のうちの最小値をとる(α+≦αcまたはαc=minα+).
(c)唯一性定理
ⒺとⓂとⓎを同時に満足するような静的応力状態または運動的変形状態の中で得られる荷重は真の崩壊荷重Pcに等しい.すなわち,真の崩壊荷重は静的および運動的許容荷重の間にある(P–≦Pc≦P+またはPc=maxP–=minP+).また真の崩壊荷重係数αcは静的および運動的許容荷重係数が等しいときの荷重係数である(α–≦αc≦α+またはαc=maxα–=minα+).
以上の基本定理を図3.21のような両端固定ばりについて説明すると次のようになる.まず.図3.21(a)の任意の静的許容応力状態を仮定して荷重係数α–を求めると,α–=2.31MP/Plが得られる.一方図3.21(c)の任意の運動的許容変形状態(崩壊機構)を仮定して荷重係数α+を求めると,α+=3.60MP/Plが得られる.よって,真の崩壊状態で得られる荷重係数αc=2.57MP/Plはα–とα+の間にある.すなわち,静的定理はⒺとⓎを満足する危険側の変形場を徐々に安全側(降伏条件Ⓨが満足される)に近づけていけば真の崩壊状態が得られることを示している.
3.5.3 平衡法と崩壊機構法
ここで,コンピューターを使用せずに手計算により崩壊荷重係数αcを求める方法を述べる.これらの方法は簡単な構造物に限定されるが,大規模な構造物の解析に便利な線形計画法(LP)による方法の基礎をなすものである.
(a)平衡法
1)原理:ⒺとⓎを用いてαc=maxα–を求める.
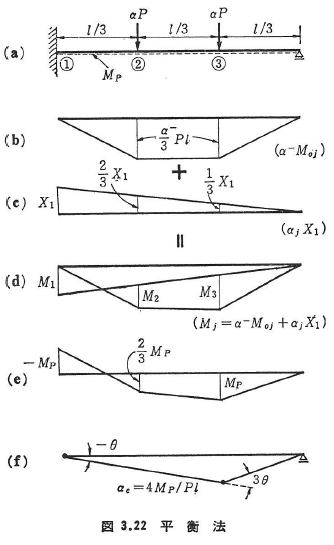
2)方法:図3.22(a)に示す一端固定ばりを例にとり説明する.
- 不静定量X1を選び,静定基本系を作る.
- 静定基本系において,外荷重のみによる曲げモーメント図(α–M0j)を図3.22(b)のように描く.
1)原理:ⒺとⓎを用いてαc=maxα–を求める.
2)方法:図3.22(a)に示す一端固定ばりを例にとり説明する.
- 不静定量X1を選び,静定基本系を作る.
- 静定基本系において,外荷重のみによる曲げモーメント図(α–M0j)を図3.22(b)のように描く.
- 静定基本系において,不静定力X1による曲げモーメント図(ajX1)を図3.22(c)のように描く.
- Ⓔ条件より合成曲げモーメント図(Mj=α–M0j+ajX1)を図3.22(d)のように描く.
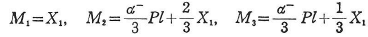
- Ⓨ条件を満足するようにmaxα–を求める.
M1=-MP,M3=MPとおくと
αc=maxα–=4MP/Pl - 崩壊時の曲げモーメント図および崩壊機構Ⓜはそれぞれ図3.22(e)および(f)のようになる.
(b)崩壊機構法
1)原理:ⒺとⓂを用いてαc=minαi+(i=1,2,…,p)を求める.ここで,αi+は,ある崩壊機構Ⓜに仮想仕事の原理Ⓔを適用して次式のように算定される.

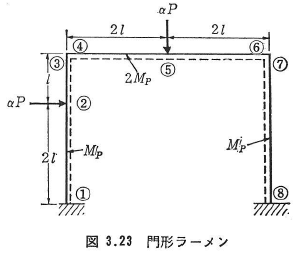
2)方法:図3.23に示す門形ラーメンを例にとり説明する.
- 各節点に番号をつける(j=1,2,…,8).
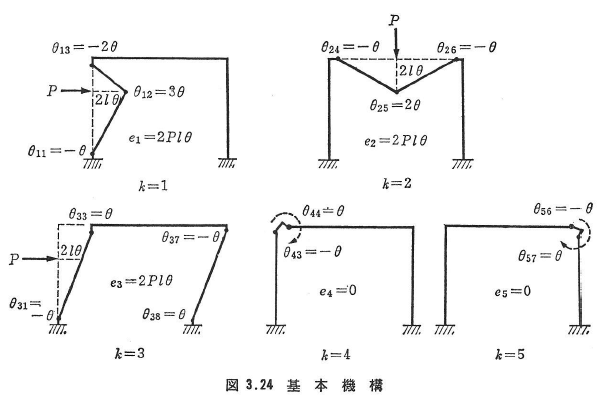
- 基本機構の数mは,全節点数s=8および不静定次数n=3であるので,m=s-n=5個となる.これらは図3.24に示すようなθkjとek(k=1,2,…,5)の値をもつ2つのはり機構,1つの層機構および2つの節点機構として与えられる.ただし,θkjの符号は曲げモーメントと同じく図3.23の点線側に引張を生ずる方向を正とする.通常,便宜的にヒンジの位置が点線側の方へ移動する場合を正とする.
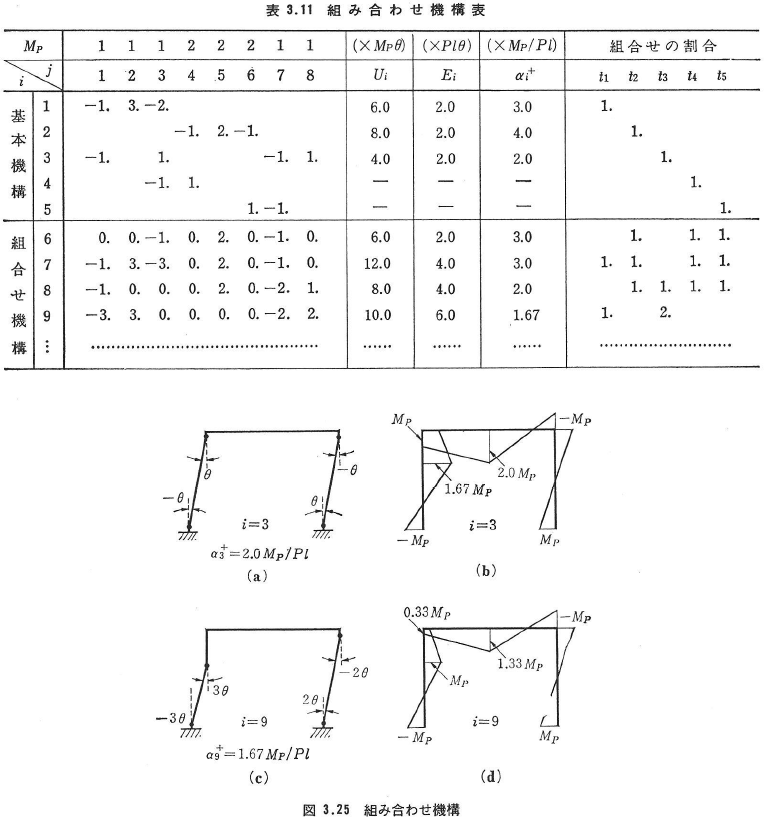
- まず図3.24の基本機構を崩壊機構(i=k=1,2,…,5)と考え,式(3.98)を用いてαi+を求める(表3.11参照).
- αi+が最小となるi=3(図3.25(a))のⓎをチェックすると,図3.25(b)のようにⓎ条件を満足していない.
- よって,表3.11のような組み合わせ機構表を用いて,組み合わせ機構(i=6,7,8,9,…)のαi+を求める.最小となるi=9(図3.25(c))のⓎ条件をチェックすると図3.25(d)のように満足されている.よって,真の崩壊荷重係数はαc(=α9+)=1.67MP/Plとなる.
なお,組み合わせ機構(i=m+1,…,p)を作るときはなるべく塑性ヒンジを消去するように組み合わせる.これは内力仕事Uiをなるべく小さくし,外力仕事Eiを大きくするように組み合わせれば,荷重係数αi+が小さくなるからである.
また組み合わせ機構は2自由度以上となり,可能な組み合わせ機構の最大の数は,
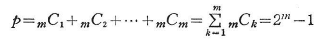
となる.しかし,実際に起こりうる可能な崩壊機構の数prはpよりはるかに少ない(pr≪p).
3.5.4 線形計画法(LP)による計算
ここでは,コンピューターを利用して大規模構造の崩壊荷重を組織的かつ効率的に求める方法を述べる.3.5.2で述べた塑性解析の基本定理は,応用数学の分野で発達した線形計画法(LP)を利用するうえで極めて便利ある.それは,塑性解析が最大,最小値を求める問題であり,また,単純塑性理論に基づくため目的関数および制約条件とも未知変数の一次式で表すことができるからである.
(a)静的アプローチ(Static Approach)
ⒺとⓎを満足する静的許容な曲げモーメント分布に対応する荷重係数α–のうちの最大値が真の崩壊荷重係数であるから,式(3.94)と式(3.97)を用いて次のようなLP問題として定式化される.

上式を解くには通常シンプレックス法が用いられるが,未知の変数が常に非負であるという条件が必要である.よって,上式にMj=Mj+–Mj–という非負の変数Mj+(≧0),Mj–(≧0)に変換して解くこととなり,式(3.99)を最小化問題としてコンピューター用のシンプレックス表に展開すると表3.12のようになる.
(b)運動的アプローチ(Kinematic Approach)
ⒺとⓂを満足する運動的許容な変形機構に対応する荷重係数α+のうちの最小値が真の崩壊荷重係数αcであるから,式(3.96)および式(3.98)を用いて次のようなLP問題として定式化される.
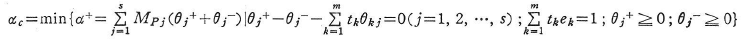
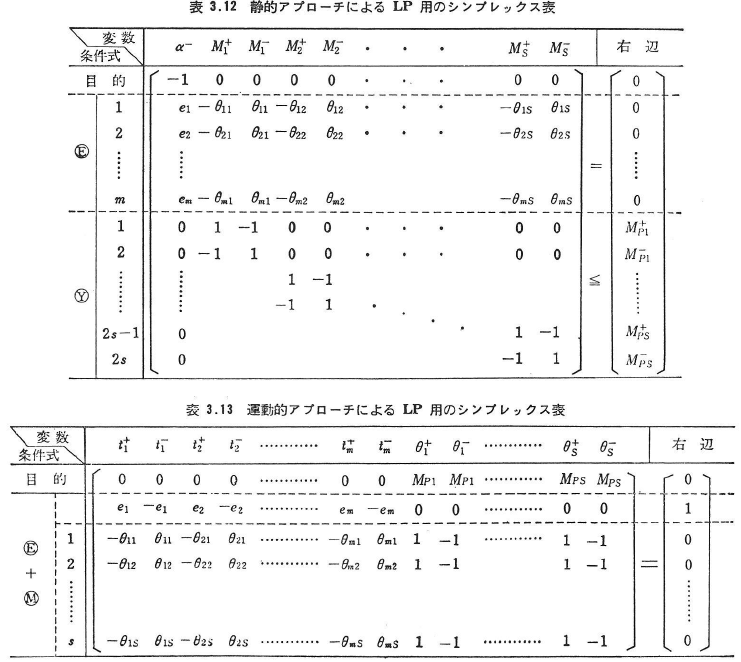
式(3.100)はある組み合わせ機構が形成される中で,単位の外力仕事に対する塑性ヒンジのなす内力仕事を最小にすると真の崩壊荷重係数αcが得られることを示している.ただし,θj+,θj–=節点jの仮想回転角θjの正側および負側の絶対値(θj+≧0,θj–≧0).また,Ei(=![]() tkek)=1としたのは,組み合わせ機構において作用荷重のなす外力仕事が常に正(Ei>0)であることと,静的定理による式(3.99)との双対性を満足させるため(変数α–に対応する係数は1)である.式(3.100)をコンピューター用のシンプレックス表に書くと表3.13のようになる.なお,tkもtk=tk+–tk–として非負の変数(tk+≧0,tk–≧0)に変換している.
tkek)=1としたのは,組み合わせ機構において作用荷重のなす外力仕事が常に正(Ei>0)であることと,静的定理による式(3.99)との双対性を満足させるため(変数α–に対応する係数は1)である.式(3.100)をコンピューター用のシンプレックス表に書くと表3.13のようになる.なお,tkもtk=tk+–tk–として非負の変数(tk+≧0,tk–≧0)に変換している.
3.5.5 組合せ応力を受ける塑性解析法
前項までは曲げモーメントのみを受ける骨組構造を対象としたが,ここでは曲げと軸力,曲げとねじり,2軸曲げとねじりと軸力などの組合せ応力を受ける骨組構造の塑性解析法を述べる.材料は剛塑性体とし,組み合わせ応力に関する非線形な降伏条件は線形化近似できるものとする.
(a)基本条件
- 降伏条件Ⓨ
組み合わせ応力を受ける断面の厳密な降伏条件をいくつかの線分(面)で近似化すると,部材要素iに対する降伏条件式は次のように表される.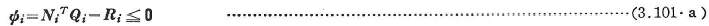
ここに,Φi:要素iの降伏凸多面体を表す降伏関数ベクトル,Ni:要素iの降伏凸多面体の外向き単位法線マトリックス,Qi:要素iの作用断面力ベクトル,肩字Tは転置マトリックスを示す.Ri:要素iの降伏凸多面体の原点から降伏線(面)までの距離を示すベクトル(塑性容量ベクトル).
例えば,曲げとねじりを受ける断面の降伏曲線は一般的に図3.26のような円となるが,これを実践のような八角形で近似すると,降伏線2の単位法線ベクトルはN2T={0.384 0.924}で,塑性容量はR2=0.924となる.また,作用断面力Qiが降伏線(面)上にあるときは,Qiに対応する作用変形速度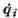 がその降伏線(面)上の外向き単位法線マトリックスに比例するという塑性流れ則が成立する.すなわち,
がその降伏線(面)上の外向き単位法線マトリックスに比例するという塑性流れ則が成立する.すなわち,
ここに,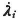 :降伏凸多面体に関与する塑性乗数ベクトルで非負の値をもつ(
:降伏凸多面体に関与する塑性乗数ベクトルで非負の値をもつ(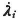 ≧0).
≧0).
さらに,塑性乗数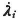 は作用断面力が降伏限界に達した(Φi=0)のちに生じ(
は作用断面力が降伏限界に達した(Φi=0)のちに生じ(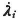 >0),それ以前(Φi<0)には発生しない(
>0),それ以前(Φi<0)には発生しない(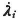 =0)という条件より次式がえられる.
=0)という条件より次式がえられる.
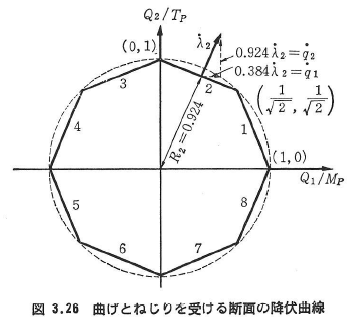
- 崩壊機構条件Ⓜ
部材要素iの作用変形速度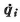 は,構造物の独立な節点変位速度
は,構造物の独立な節点変位速度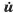 と幾何学的に結合する
と幾何学的に結合する をすべての要素に適用して次式を得る.
をすべての要素に適用して次式を得る.
ここに,C:構造全体の適合マトリックス.
式(3.101・b)をすべての要素に拡張したうえで式(3.102)と等置すると次式のような崩壊機構条件がえられる.
また,崩壊機構において作用荷重のなす外力仕事は常に正である.(単に1とおくと)ことより次式が成立する.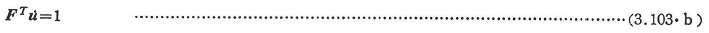
ただし,F:節点に作用する外荷重ベクトル. - つり合い条件Ⓔ
構造全体において作用断面力Qが節点に作用する崩壊荷重αFとつり合うという条件であり,式(3.102)に反傾定理を適用して次式をえる.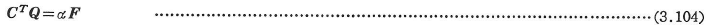
(b)組み合わせ応力を受ける場合の基本式
- 静的アプローチ
ⒺとⓎを満足する静的許容応力場に存在する荷重係数のうちの最大値が真の耐力であるから,式(3.101・a)をすべての要素に拡張したものと式(3.104)を用いて次式がえられる.
- 運動的アプローチ
ⒺとⓂを満足する運動的許容変形場に存在する荷重係数のうちの最小値が真の耐力であるから,ある崩壊機構(式(3.103・a))において塑性容量のなす内力仕事と崩壊荷重のなす外力仕事が等しいという条件(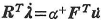 )より次式をえる.
)より次式をえる.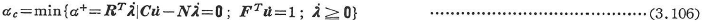
式(3.105)と式(3.106)は互いに双対性を満足している. - 唯一性アプローチ
式(3.105)または式(3.106)にクーン-タッカー(Kuhn-Tucker)条件を適用すると,塑性解析に必要かつ十分な条件が次のようにえられる.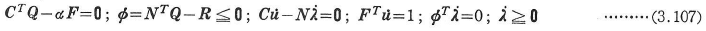
上式を同時満足するαを求められれば,それが真の崩壊荷重係数αc(=α)である.
