Contents
1.6.1 仕事とエネルギー
（a）仕事と補仕事
質点が力Fの作用のもとにdrだけ変位すると，力Fによる仕事dWは次のように定義される．
また，このときA点にあった質点がB点に変位したとすると，力Fによる仕事は次のようになる．
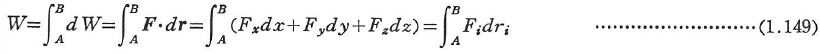
変形する固体に対しては，表面力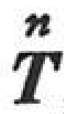
，物体力
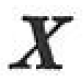の作用のもとに，物体の各点がduだけ変位したとすると，これらの外力のなす仕事は次のように与えられる（図1.30）．
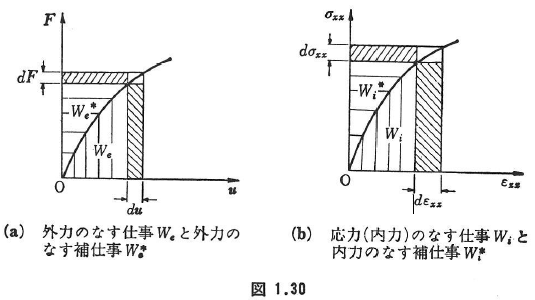
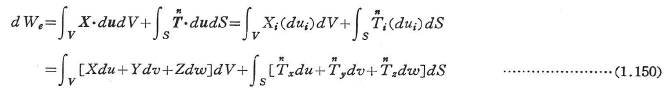
応力σxx，σyy，…，σyz，σzxのもとに，ひずみがdεxx，dεyy，…，dεyz，dεzxだけ増加したとすると単位体積当たり応力（内力）のなす仕事は次のように与えられる（図1.30）．
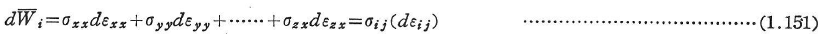
物体全体に対しては次のようになる．
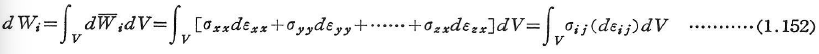
補仕事は仕事に対する相補的な関係として次のように定義される（図1.30）．
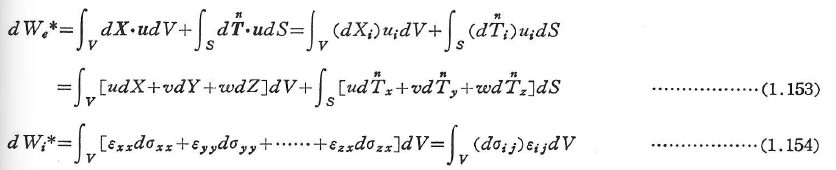
（b）ポテンシャルエネルギーと補ポテンシャルエネルギー（complementary potential energy）
エネルギーは外部に対して仕事をする能力であり，その量は外部に対してなす仕事量で計られる．仕事はエネルギーの形が変わったことによってなされるので，一般にはエネルギーの変化量だけが問題となる．
式（1.149）で定義される仕事量が保存系，すなわち，A点からB点に至る経路に左右されないとすると，
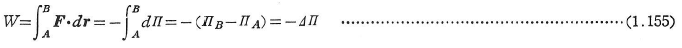
ここに，
である．このような
を系のポテンシャルエネルギーとよぶ．すなわち，「ポテンシャルエネルギーの変化は負の仕事量に等しい」ことになる．
変形する物体のポテンシャルエネルギーは，微小変形で準静的条件のもとで次のように定義される．
外力のポテンシャルエネルギーHは，物体が自然状態からＩ状態に変化する間に外力のなした仕事量に負の符号を付けたものとして定義される．
（c）ひずみエネルギーと補ひずみエネルギー（complementary strain energy）
自然状態から変形した状態で物体内に貯えられる内部エネルギーはひずみエネルギーとよばれる．
自然状態から状態Ｉに変形した物体の体積要素dVに貯えられる全ひずみエネルギーは，次のように与えられる．
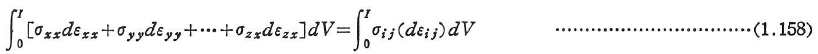
この積分の値は経路には左右されないので，単位体積当たり内力のなす仕事dWiは，ポテンシャル関数U0の完全微分で表される．
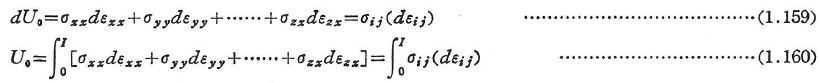
ここに，U0は，εxxI，εyyI，…，εzxIの関数であり，単位体積当たりのひずみエネルギー，ひずみエネルギー関数，あるいはひずみエネルギー密度とよばれる．
一方，dU0は完全微分であるから，
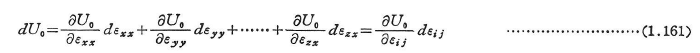
となり，この式と式（1.159）を比較すると次式を得る．
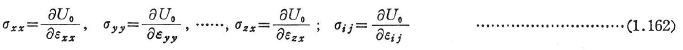
全ひずみエネルギーは次のようになる．
線形弾性体の場合，
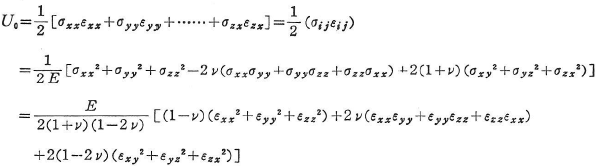
である．これは，クラペイロン（Clapeyron）のひずみエネルギーとよばれている．
補ひずみエネルギー密度は次のように定義される．
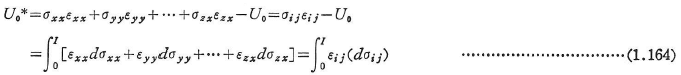
ここに，積分は自然状態から状態Ｉまで行う．U0＊は，補ひずみエネルギー密度とか単位体積当たりの補ひずみエネルギーともよばれる．
dU0＊は完全微分であるので，
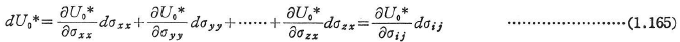
となり，式（1.164）から得られる
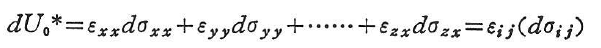
と比較して，次式を得る．
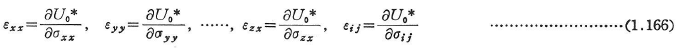
全補ひずみエネルギーU＊は，次のように与えられる．
線形弾性体の場合には，U0＊＝U0となる．
（d）全ポテンシャルエネルギーと全補ポテンシャルエネルギー
全ポテンシャルエネルギーは，外力のポテンシャルエネルギーとひずみエネルギーの和として定義される．
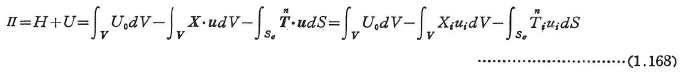
全補ポテンシャルエネルギーは外力の補ポテンシャルエネルギーと補ひずみエネルギーの和として定義される．
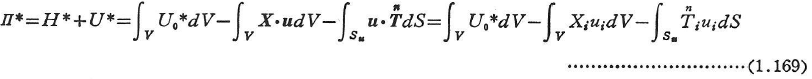
これらは，単にポテンシャルエネルギーあるいは補ポテンシャルエネルギーとよばれることも多い．
1.6.2 エネルギーに関する諸定理
（a）変分
変位uがSu上の境界条件および変位の連続条件を満足しつつ（以下これを変形適合という）u+δuまで変化したとする．そのときの仕事の増分ΔWeは次のように与えられる．
ここに，
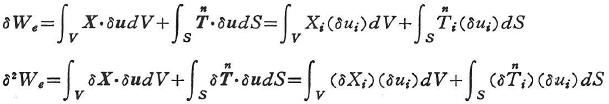
はそれぞれ仕事の第1変分および第2変分とよばれる．O（δ3）は三次以上の高次項を表す．
変位の変化に応じて，ひずみがεxx，εyy，…，εzxからεxx+δεxx，εyy+δεyy，…，εzx+δεzxに変化したとすると，ひずみエネルギー増分ΔUは次のように与えられる．
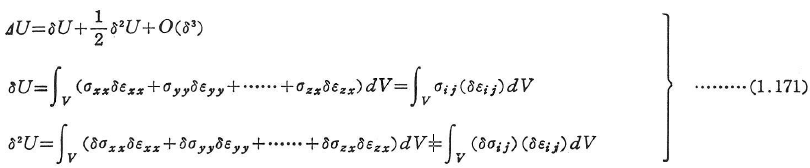
ここに，δU，δ2Uはひずみエネルギーの第1，第2変分である．
表面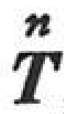力と物体力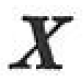がつり合い条件およびSσ上の境界条件を満たしつつ（以下静力学的（つり合い）許容という）
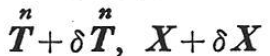となり，これに応じて応力もσxx，σyy，…，σzxからσxx+δσxx，σyy+δσyy，…，σzx+δσzxとなったとする．このとき補仕事，補エネルギーの増分は次のように与えられる．
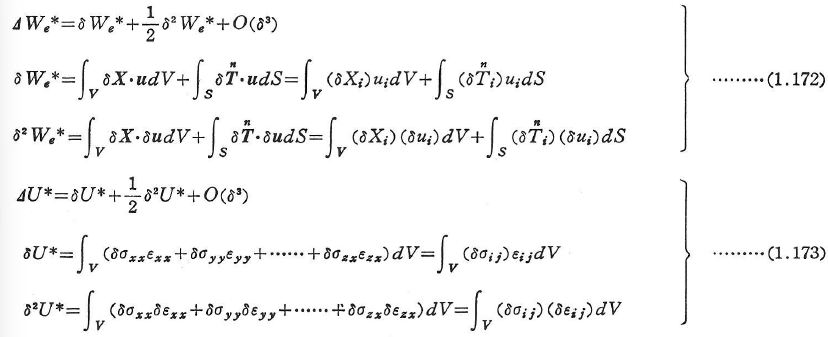
（b）ポテンシャルエネルギー停留および最小の原理
つり合い状態にある弾性体（非線形でもよい）を考える．変形適合な任意の変位δuに伴う外力の仕事は内力（応力）の仕事に等しく，内力の仕事はひずみエネルギーとして貯えられる（式（1.204）参照）．よって，
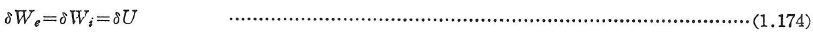
あるいは，
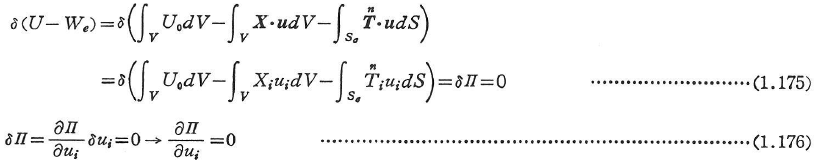
これは次のことを意味している．
「つり合い状態にある弾性体において，変形適合なすべての変位場のうちで，つり合い条件を満足するような応力場と関連づけられるものが，全ポテンシャルエネルギーを停留値とする」（全ポテンシャルエネルギー停留の原理）．
これは次のように言い替えることができる．「すべての変形適合な変位のうちで，つり合い状態をも満足するもの，すなわち真の変位が全ポテンシャルエネルギーを停留値とする」．
さらに，つり合い条件も境界条件もすべて満たす真の変位をu，変形適合な任意の変位をu=u+δuとすると，両者に対する全ポテンシャルエネルギーの差は
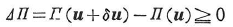
あるいは，
であることが示される．これより，
「弾性体に対し，すべての変形適合な変位のうちで，安定なつり合い条件をも満たすもの，すなわち，真の変位は全ポテンシャルエネルギーを最小とする」（全ポテンシャルエネルギー最小の原理）．「真の解は全ポテンシャルエネルギーを最小とする」．
（c）補ポテンシャルエネルギー停留および最小の原理
変形適合状態にある弾性体（非線形でもよい）を考える．つり合い条件を満たしつつ，物体力と外力が
だけ変化し，それに対応して応力がδσxx，δσyy，…，δσzxだけ変化したとすると，外力のなす補仕事は内力のなす補仕事と等しく，補ひずみエネルギーとして貯えられるので，次の関係を得る（式（1.205）参照）．
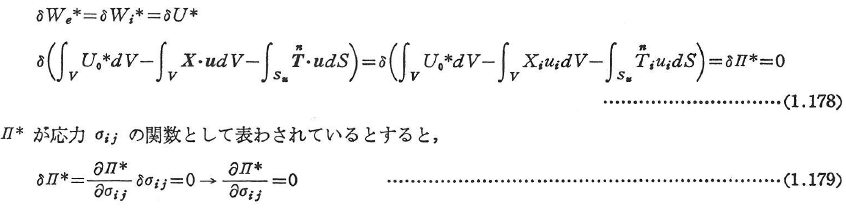
これより「外力の境界条件を満たし，かつ，つり合い状態にあるすべての物体力と外力および応力のうち，変形適合な変形とひずみ場に対応するものが全補ポテンシャルエネルギーを停留値とする」（全補ポテンシャルエネルギー停留の原理）が得られる．
さらに弾性体がつり合い条件および境界条件を満たす真の状態にあるとし，そのときの応力をσxx，σyy，…，σzxとする．一方，静力学的に許容な任意の応力を
とする．それぞれの状態に対する全補ポテンシャルエネルギーの差は，
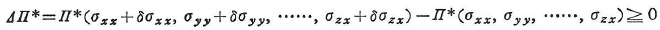
あるいは，
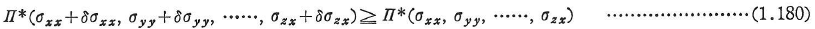
であることが示される．これより，「つり合い条件と力で与えられた境界条件を満たす応力のうちで，安定な変形適合な変形に対応するもの，すなわち，真の応力状態が全補ポテンシャルエネルギーを最小とする」（全補ポテンシャルエネルギー最小の原理），「真の解は全補ポテンシャルエネルギーを最小とする」．
1.6.3 カスティリアノ（Castigliano）の定理
Castiglianoの定理は，全ポテンシャルエネルギーおよび全補ポテンシャルエネルギー停留の原理の特別な場合である．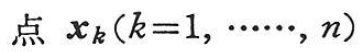
に集中力Pkが作用しているとすると，全ポテンシャルエネルギーおよび全補ポテンシャルエネルギーは次のようになる．
停留原理（式（1.176），（1.179））より，
ここに，Uはukの，U*はPkの関数で表されている．uk(n)，Pk(n)はそれぞれ，uk，Pkのn方向成分を意味する．なお，ukとして変位拘束を，Pkとしては拘束力（不静定力）を解除したものであってもよい．
（a）Castiglianoの第2定理
Castiglianoの第2定理は式（1.181）より次のように表現される．系のひずみエネルギーUがn個の与えられた一般化外力（力・モーメント）Pk（k=1,2,…,n）のもとで，これに対応するn個の独立な一般化変位（変位・回転）uk（k=1,2,…,n）の関数として表されるならば，ひずみエネルギーのukによる1階偏導関数は，Pkのuk方向への成分に等しい
なお，式（1.181）と式（1.162）とを比較されたい．後者は，微小要素に対するCastiglianoの第1定理と考えられる．
この定理はエンゲッサ―（Engesser）の第1定理ともよばれる．場合によっては，線形弾性体に適用した場合のみをCastiglianoの第2定理とよんで区別することもある．
1.6.4 最小仕事の原理
この原理は，式（1.182）においてPkとして不静定力を選んだ場合であり，次のように表現される．「つり合い状態にあるn次不静定系のすべての可能な不静定力Xi(i=1,2,…，n)の組のうち，これら不静定力に対応する変位δi(i=1,2,…，n)が与えられているならば，適合条件を満たすように選んだ不静定力Xiの組は，補ポテンシャルエネルギーを最小とする」．
ここに，Xi，δiは，Xi，δiの大きさを表す．
特に，δi=0，すなわち不静定力を選んだ点に変位が生じないとすれば次のようになる．
式（1.183）で表される原理は最小仕事の原理，あるいはEngesserの第2定理とよばれる．特に，線形弾性体の場合には最小仕事に関するCastiglianoの定理ともよばれる．
1.6.5 剛性影響係数と撓性影響係数
線形弾性構造では，一般化力Piと一般化変位uiが比例する．
これより，
kij，fijをそれぞれ剛性影響係数，撓性影響係数という．
一般化力，一般化変位は，式（1.181），（1.182）で与えられるので，次式を得る．
物理的意味は，「kijはuj=1他はすべて０としたときに，点iに加えるべき一般化力Pi」であり，「fijはPj=1他はすべて０としたときに，点iに生じる一般化変位ui」である．
1.6.6 相反作用の定理
（a）重ね合わせの原理
重ね合わせの原理は２つまたはそれ以上の作用が同時に生じた状態に関連して適用され，それぞれの作用による効果が独立に知られておれば，それらが同時に作用したときの効果は加算的，すなわちそれぞれの効果の和で表されることを言明したものである．
重ね合わせの原理が成立するための条件は，①系の変形は十分小さくて変形後のつり合い条件および適合条件が変形前の形状を用いて十分正確に表されること，②系は要素はすべて線形的であること，である．
（b）相反作用の定理
ベッチィ（Betti）の相反作用定理は，次のように表現される．
「線形弾性体系が異なった2つの力群の作用を受ける場合には，第1群の力が第2群の力によって生じる変位に対してなす仕事W1,2は第2群の力が第1群の力によって生じる変位に対してなす仕事W2,1に等しい」．
第1の力群を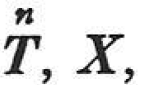
それによって生じる変位をu，第2の力群を
それによって生じる変位をu‘とすると上式は次のようにも表現される．
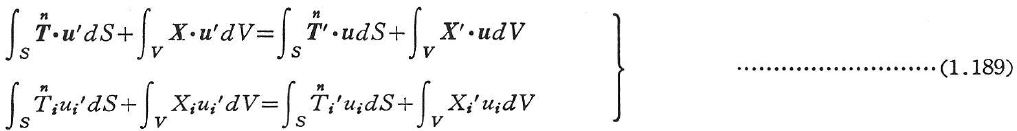
外力群として単一の集中力P，P’のみが作用すると考えると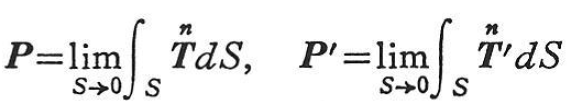
であるから，式（1.189）は次のようになる．
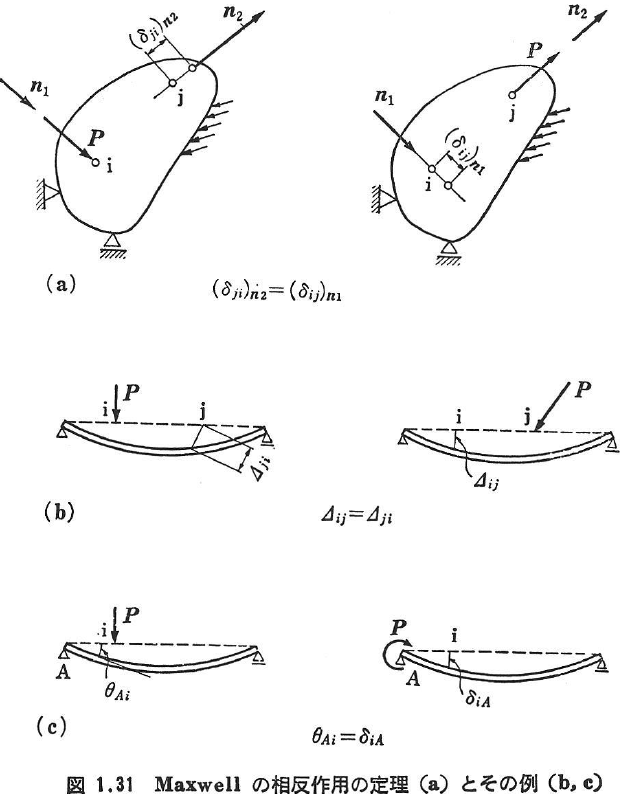
特に，P=P’とするとマックスウェル（Maxwell）の相反作用の定理を得る．すなわち，
「点jに作用する荷重（モーメント）Pによる点iのP’方向への変位（回転角）は，点iに作用する荷重（モーメント）P’による点jのP方向への変位（回転）に等しい」．
点iにPがn1方向に作用して，点jにn2方向の変位（δji)n2が生じ，点jにP’（｜P’｜＝｜P｜）がn2方向に作用して，点iにn1方向の変位（δij)n1が生じたとすると，Maxwellの定理は次のようにも表現される．（図1.31）．
1.6.7 エネルギー原理の一般化
次のように汎関数を導入する．
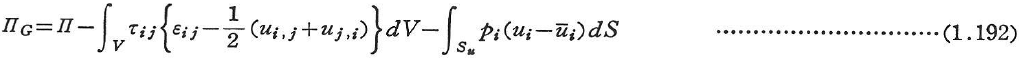
ここに，τij，piはLagrange乗数，
はSu上で与えられた関数とする．変量はui，εij，τij，piである．
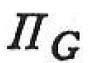の停留条件，
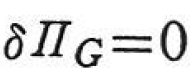より次式が得られる．
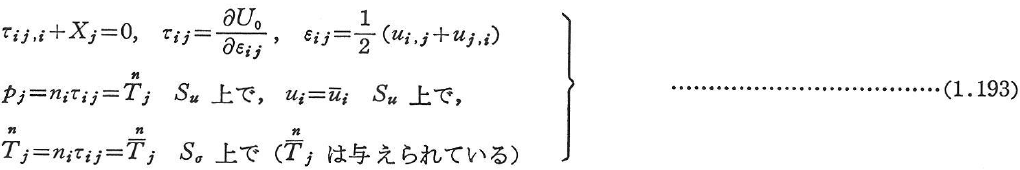
これより，τijは応力σijに，piは応力ベクトル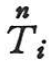
に対応することがわかる．τij，piの代わりにσij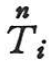，を式（1.192）に代入した汎関数を停留にすれば，弾性境界値問題のすべての基礎式，構成式および境界条件が求まる．これをフ―-鷲津（Hu-Washizu）の原理という．
新しい汎関数
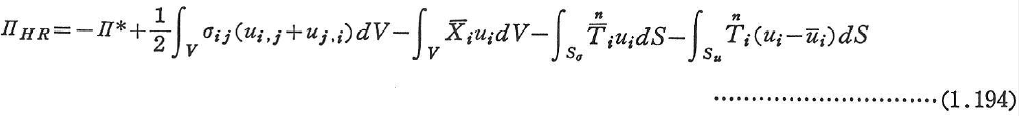
を考える．変数はui，σijである．
の停留条件，
より次式を得る．
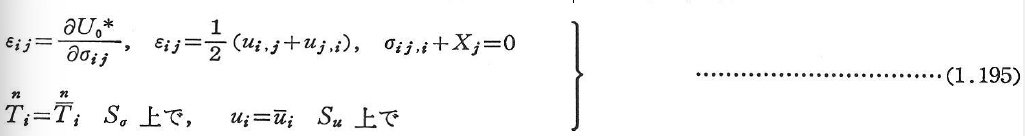
この変分原理をへリンガー-ライスナー（Hellinger-Reissner）の原理という．
以上2つの原理には変量として変位と応力が含まれているので，混合型の変分原理ともよばれる．
なお，非弾性体に対しても以上の変分原理および仮想仕事の原理（1.6.9参照）は容易に拡張することができる．その場合には一般に速度（増分）型，すなわち応力速度，ひずみ速度，速度場ならびに対応した速度型の境界条件を対象としたものとなる．
1.6.8 ハミルトン（Hamilton）の原理
運動している弾性体に対して全ポテンシャルエネルギー停留の原理を適用する．時間t1≦t≦t2で運動を考え，時刻t1，t2では変位は既知であるとすると，次の変分原理を得る．
ここに，Uは全ひずみエネルギー（式（1.163）），Hは外力のポテンシャルエネルギー（式（1.156）），Tは運動エネルギー
である．なお，ρは密度である．
すなわち，「時間t1≦t≦t2における弾性体の運動は，全動力学的ポテンシャルU-T+Hの時間積分を停留値とする」（Hamiltonの原理）．
なお，静的，すなわちT=0であれば，δ（U+H）=δΠ=0となり，式（1.175）と一致する．
1.6.9 仮想仕事の原理
（a）仮想仕事と補仮想仕事
仮想仕事は実在する力がこの力とは関係のない仮想な変位（仮想変位）を通じてなす仕事である．補仮想仕事は，実在する変位を通じてこれに無関係な仮想な力（仮想力）が作用することによってなす仕事である．
質点が力Fの作用のもとで，これとは関係ない仮想変位δrが生じたとすると，仮想仕事は次のように定義される．
質点がrだけ変位する際に仮想力δFが作用していたとすると，補仮想仕事は次のように定義される．
場合によってはδWとδW*を区別せずに仮想仕事とよぶこともある．
変形する物体に関する仮想仕事，補仮想仕事は以下のように定義される．
表面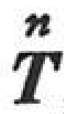力，物体力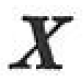のもとでつり合っている物体，すなわち，つり合い系の物体に，このつり合い系とは独立で，かつ幾何学的な境界条件および適合条件を満足する，いわゆる変形適合な仮想変位δuが生じたとすると，外力のなす仮想仕事は次のように与えられる．
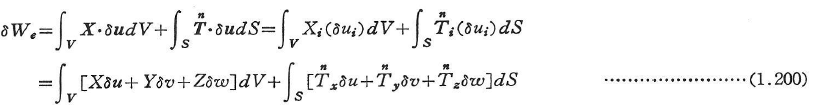
また，内力の仮想仕事は次のように与えられる．
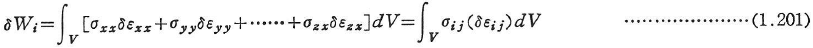
ここに，σxx，σyy，…σzxはつり合い系に，またδεxx，δεyy，…δεzxは変形適合系に属している．
外力による補仮想仕事δWe*および内力による補仮想仕事δWi*はそれぞれ次のように定義される．
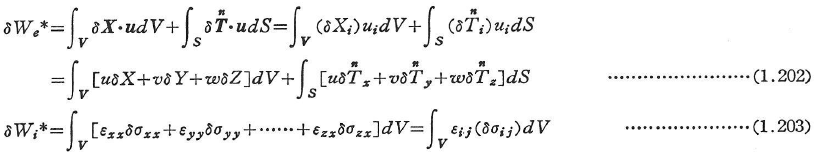
ここに，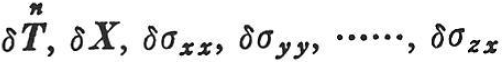
はつり合い系に属し，
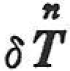は力学的な境界条件を満たすもの，すなわち，静力学的な仮想表面力である．また，εxx，εyy，…εzx，uは変形適合系に属するものである．
（b）仮想仕事の原理
仮想仕事の原理は次のように表現される．
「系がつり合い状態にあれば，変形適合なすべての仮想変位に対して，外力の全仮想仕事は内力の全仮想仕事に等しい」．すなわち，
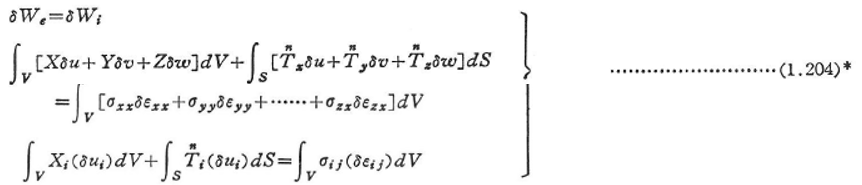
逆に，「許容なあらゆるδuiに対して上式が成立すれば，系はつり合い状態にある」．
（c）補仮想仕事の原理
補仮想仕事の原理は次のように表現される．
「系が変形適合状態にあれば，つり合い状態を保ち，かつ静力学的に許容な仮想な物体力，外力および応力に対して，外力の全補仮想仕事は内力の全補仮想仕事に等しい」．すなわち，
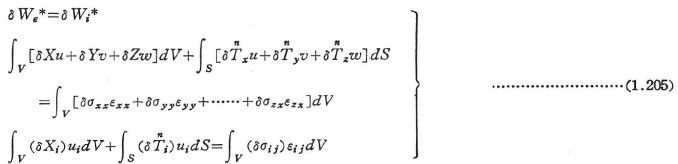
逆に，「許容なあらゆる
とδσijに対して上式が成立すれば，系は変形適合状態にある」．
（d）単位（仮想）変位法
式（1.204）において，物体表面に集中力Pk=Pδ(x–xk)が作用している場合を考える．その点の仮想変位をδukとし，他の集中力の作用点での仮想変位をすべて０とすると，
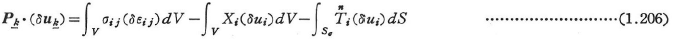
を得る．kに対しては総和規約（1.2.1（d）3参照）を適用しない．特に，δuk=nk（δukとして，uk方向への単位変位）とすると，その方向に働く力（の大きさ）Pk(n)は，次のように与えられる．
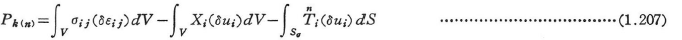
δukとして，変位・回転角などを考えれば，それに対応した力・モーメントなどが求まる．これを単位（仮想）変位法という．式（1.207）ではσijは実際の荷重，物体力の下で生じている実応力とか初期応力，δui，δεijはδuk=nkにより生じる仮想の変位，ひずみであることに注意されたい．
（e）単位（仮想）荷重法
式（1.205）において，物体表面だけに仮想の集中力δPkのみが点xkに作用したとすると，
を得る．kに関して総和規約を適用しない．特に，δPk=nk（δPkとして，nk方向への単位荷重）を取ると，その方向への変位uk(n)は次のように与えられる．
δPkとして，力，モーメントなどを考えれば，それに対応した変位，回転角などが求まる．これを単位（仮想）荷重法という．上式中，εijは実際の荷重，温度変化などにより生じているひずみとか初期ひずみ，δσijは，δPk=nkにより生じた仮想の応力であることに注意されたい．