式(8.5)の右辺のτA0,τB0は,図8.4(d)に示したように中間荷重による両端の接線角である.したがって,荷重が与えられるとτA0,τB0は,モールの定理によると,弾性荷重を載せた共役ばりの両支点でのせん断力として求められるから,荷重項CAB,CBAは次の[例題8.1]のように,式(8.5)から容易に計算される.
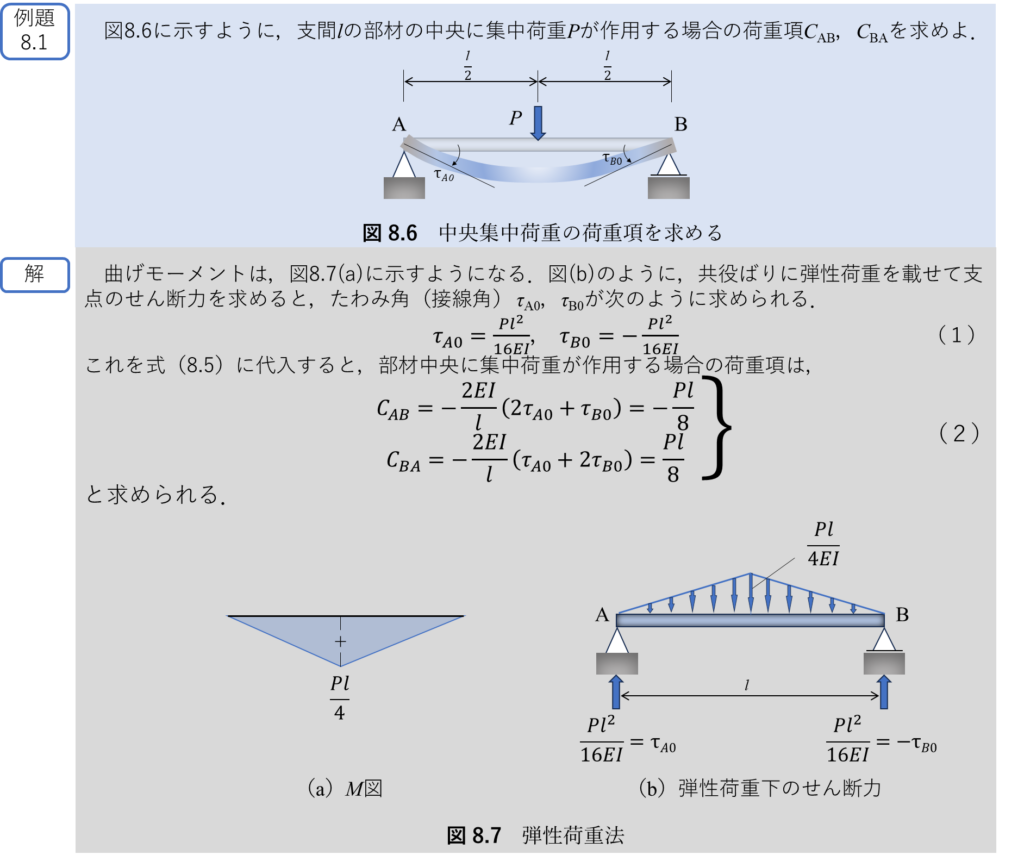
計算でよく遭遇する荷重条件に対して,CAB,CBAをあらかじめ計算しておくと便利である.代表的な荷重項の例を表8.1に示す.表の上から3番目までの荷重条件の場合の荷重項を記憶にとどめておくだけで,多くの問題を解くことができる.
表8.1 荷重項CAB,CBAの値の例
| 荷重条件 | CAB | CBA |
|---|---|---|
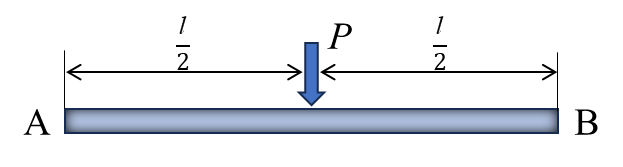 | –Pl/8 | –CAB |
 | –Pab2/l2 | Pa2b/l2 |
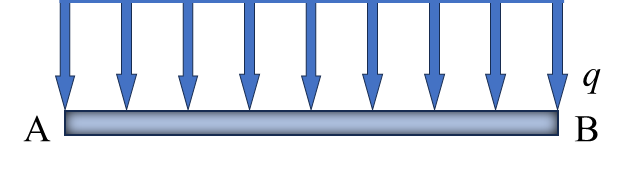 | –ql2/12 | –CAB |
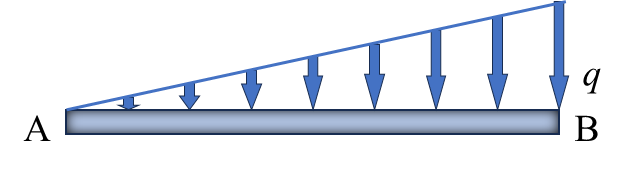 | –ql2/30 | ql2/20 |
 | M/4 | CAB |
 | Mb(2l-3b)/l2 | Ma(2l-3a)/l2 |
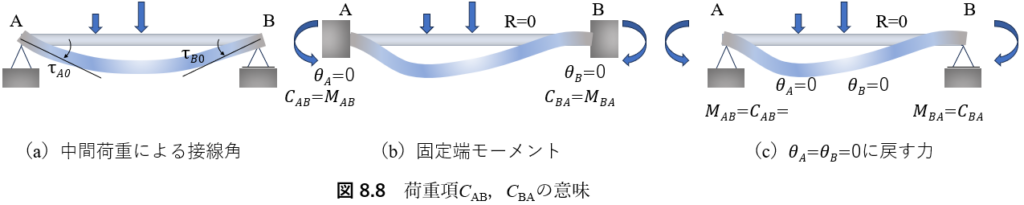
ここで,この荷重項CAB,CBAの意味を少し考えてみよう.まず,式(8.6)において,θA=θB=R=0とおくとMAB=CAB,MBA=CBAとなり,図8.8(c)のようになる.すなわち,CABおよびCBAは,図(b)に示すように,部材の両端を固定端とみなしたときに荷重によって支点に生じるモーメントと考えることができるので,固定端モーメントとよばれる.また,図(c)のθA=θB=0の状態は,中間荷重によって生じる両端の接線角τA0,τB0(図(a)参照)を端モーメントでちょうど0に引き戻したと考えても得られるので,CAB,CBAは中間荷重によって生じる両端の接線角τA0,τB0をちょうど0に引き戻すために加えるべき端モーメントとも定義される.
ここで演習問題8.1を解いてみよう.
