Contents
4.5.1 中間荷重を受ける等断面柱
(a)中間部で単一集中荷重を受ける柱(図4.5)
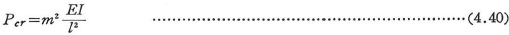
ここに,座屈係数mは荷重の作用点および上下端の境界条件によって決まる.荷重が柱中央に作用するとき,mは境界条件によって次の値をとる.

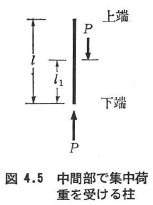
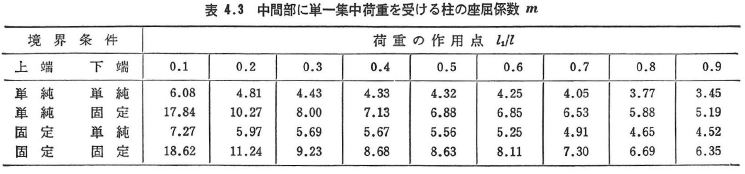
柱中間部の任意の点に荷重が作用するときのmの値を表4.3に示す.
(b)上端および中間部の2つの集中荷重を受ける柱(図4.6)
両端単純支持でl1=l2のとき,

ここに,座屈係数mは次の式から求まる値の最小値を用いる.
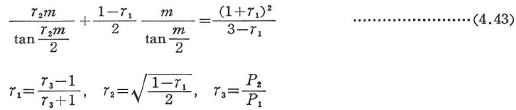
上端自由,下端固定支持でl1=l2のとき,
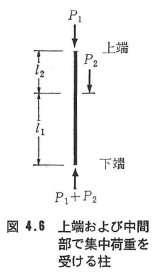

ここに,
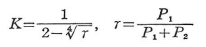
上端自由,下端固定支持で,荷重が任意の点に作用するときの座屈荷重は次の座屈条件式を満たすP1+P2の値の最小値として求まる.

ここに,
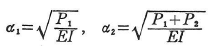
(c)全長にわたって等分布荷重を受ける柱(図4.7)

座屈係数μの値を表4.4に示す.
(d)分布荷重を受ける柱
分布荷重を受ける柱の座屈荷重を,境界条件,荷重条件とともに表4.5に示す.
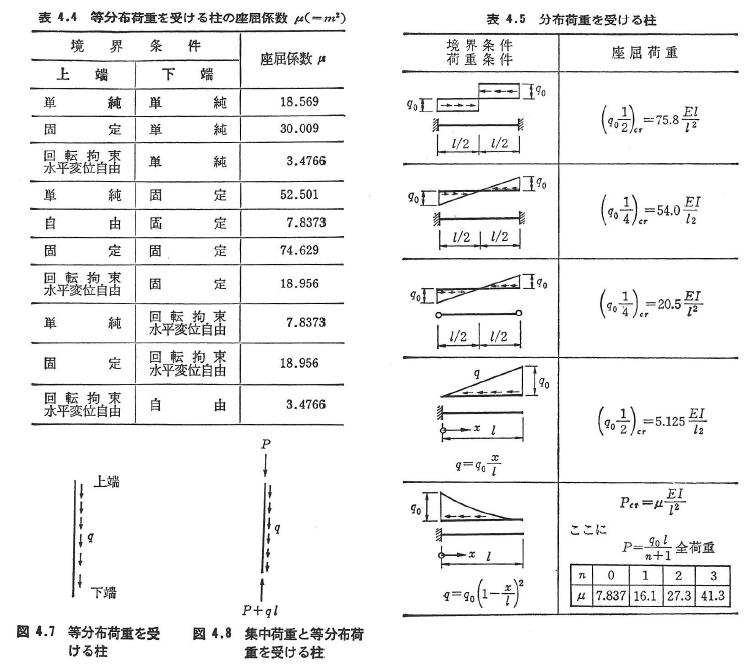
(e)上端に作用する集中荷重と全長にわたって等分布する荷重を受ける柱(図4.8)

座屈係数μの値は境界条件によって次の値をとる.

4.5.2 中間荷重を受ける変断面柱
(a)上端および断面変化部の2つの位置で集中荷重を受ける柱(図4.9)

座屈係数mの値は境界条件によって決まる次の式の最小根として求まる.

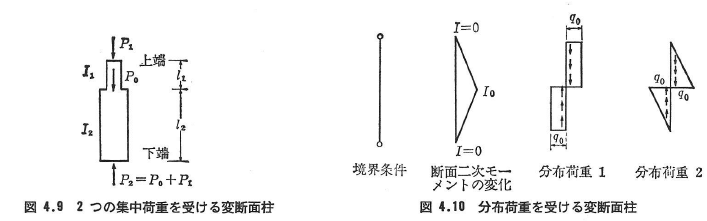
(b)分布荷重を受ける変断面柱(図4.10)
図4.10に示す両端で単純支持され,断面二次モーメントが両端で0,中央部で最大となる柱に両端から中央部に向かう等分布荷重が作用しているときの座屈荷重は次のように表される(分布荷重1).

分布荷重の値が両端で0,中央部で最大となり,その間は直線変化するとき(分布荷重2).

