ここでは，直接剛性法というコンピュータ演算に適した剛性マトリクスの誘導と演算法を学ぶ．方法はほかの章とほぼ同じであるが，部材軸方向にとった部材（局所）座標系（local system）との間と，構造物全体に都合良いようにとった全体（基準）座標系（global system）との間の座標変換行列を用いる点が異なる．
　まず，トラス部材の剛性マトリクスを求めておこう．先に示した図6.4(a)において，節点１，２の間にあるバネを，長さL，断面積A，ヤング率Eのトラス部材で置き換えたとし，節点２が固定され，力x1が作用している状態を考える．力と変位の関係は，応力とひずみの関係σ＝Eεにσ＝x1/A,ε＝u1/Lを代入して

となる．この式より，EA/Lがバネの場合のkに対応することがわかるので，式(6.9)は

と書ける．これが，x軸が部材軸に一致した部材座標系に対するトラス部材の剛性マトリクスである．
　次に，図6.9に示すように，任意方向を向くトラス部材（k=EA/L）について，全体座標系（X，Y）とx軸が部材軸に沿った部材座標系（x,y）を設定し，全体座標に対するこの部材の剛性マトリクスを座標変換の考え方を使って求める．ここで，X軸は，右向き水平方向とする．Y軸は，重力場における構造物の下向きのたわみが正になるように考えて，鉛直下向きにとる．X軸とx軸のなす角をθとする．この場合，θの符号はX軸を時計回りに回転させてx軸に重なるように測った場合を正とする．節点番号はx軸の原点に近い側をi，遠い側をjとする．

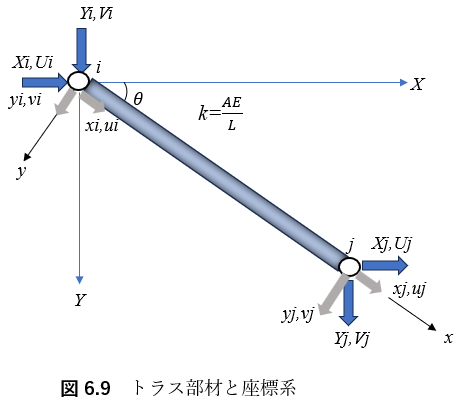
　節点変位と節点力は，局所座標に関する量を小文字で，全体座標に関する量を大文字で表すことにし，図示のように記号と正方向を定義する．
　部材ijをx方向の単一バネと考えると，いままでの結果を用いて，剛性方程式は

となる．ここで，y方向の力とモーメントのつり合いより，yi=yj=0となることを考慮すると，次のように４×４の行列に拡張できる．

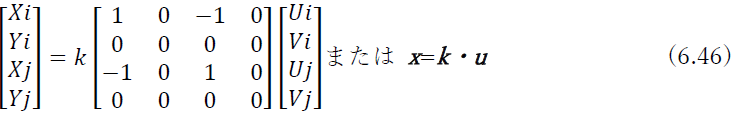
　次に，（x,y）方向の量と（X,Y）方向の量の関係を求める．まず，図6.10(a)に示すように，節点iがi‘に変位した場合を考えると

となり，同様に節点jに関しても

の関係が得られる．これを行列表示すると

となる．節点力に対しても同様に

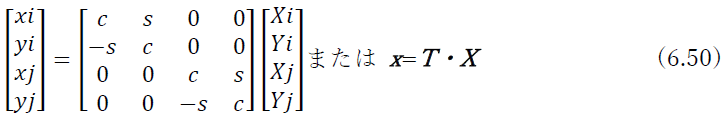
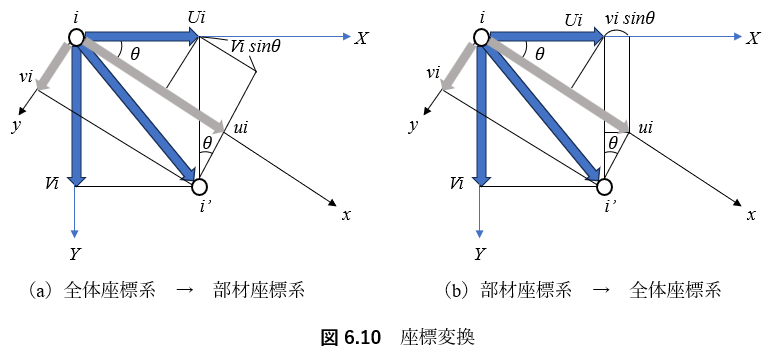
となる．この行列Tのことを全体座標系から部材座標系への座標変換行列という．
　ところで，いま，逆に（X,Y）系の量を（x,y）系の量で表してみると，図6.10(b)を参考にして

となる．これを行列表示すると

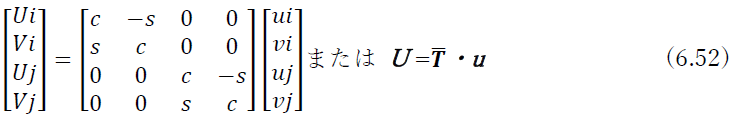
となる．ここでを式を式(6.49)のTと比較してみると，はTの転置行列T^Tになっていることがわかる．一方，式(6.49)を解くと

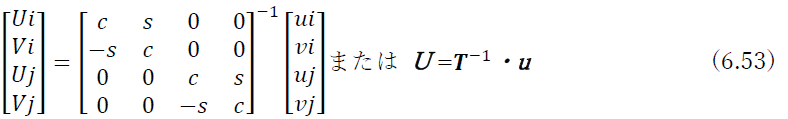
となる．
　式(6.49),(6.52),(6.53)を比較することにより，結局

という関係が得られる．すなわち，一般に座標変換行列の逆行列は転置行列になる．転置行列は簡単に得られるから，座標変換行列のこの性質は便利に用いられる．
　さて，いま，式(6.46)の左辺のxに式(6.50)を，右辺のuに式(6.49)を代入すると

となる．両辺の左からT^-1をかけると

となる．T^-1T=I，T^-1＝T^Tを考慮すると

となる．ここで

とおくと

となる．すなわち，部材座標系に関する剛性マトリクスkが式(6.46)のように与えられると，式(6.49)で与えられる変換行列Tを用いて，全体座標系の剛性方程式である式(6.59)を簡単に導くことができる．
　式(6.57)を具体的に書くと

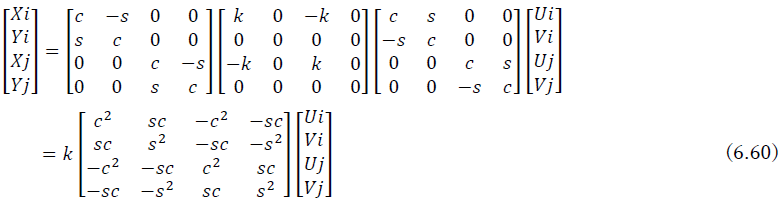
となり，この結果は式(6.42)に一致する．
　式(6.59)で与えられる剛性方程式は，一部材についてのものであるが，多くの部材を有する構造物の解析も，式(6.59)の重ね合わせで構造全体の剛性方程式をつくることができる．さらに，直列バネの解法と同様に，構造全体の剛性方程式に境界条件を考慮して解くことにより，未知変位が求められる．部材軸方向の伸び量を，求められた未知変位より計算することで，部材力Nは

と表せる．これを行列表示して次式を得る．