本節では,非減衰自由振動(固有振動)の解法について説明する.
3.6.1 エネルギー法
一次元連続体の自由振動変位uを,座標xと時間tの関数として次式のように表すことができる.

ここに,pを固有円振動数といい,固有振動数fはf=p/2πで与えられる.
非減衰自由振動ではエネルギー保存則が成り立つので,振動体のポテンシャルエネルギーVと運動エネルギーTのそれぞれの1周機関についての平均値は相等しく,また,それらの最大値も等しくなる.そこで,u(x,t)によるVとTを
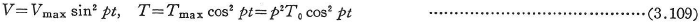
と表し,振動モード![]() を適当な関数で近似すれば,次式で固有円振動数pを求めることができる.
を適当な関数で近似すれば,次式で固有円振動数pを求めることができる.
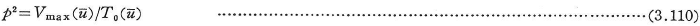
上式は,![]() を固有関数とするRayleigh商であり,
を固有関数とするRayleigh商であり,![]() の近似度よりも精度のよい振動数が求められるが,pの近似値は真の値よりも常に大きくなる.
の近似度よりも精度のよい振動数が求められるが,pの近似値は真の値よりも常に大きくなる.
基本振動数(一次振動数)を求める場合には,![]() の近似関数として静荷重による変位を用いると,比較的精度のよい値がえられる.しかし,高次振動では
の近似関数として静荷重による変位を用いると,比較的精度のよい値がえられる.しかし,高次振動では![]() を仮定することが困難であるので,次の方法を用いる.
を仮定することが困難であるので,次の方法を用いる.
境界条件を満足する数個の一次独立な関数Φi(x)とパラメーターaiを用いて,振動モードを次式で仮定する.

弾性体のポテンシャルとしてひずみエネルギーUを考える.VmaxとTmaxは,式(3.111)を用いると一般的に次のaiに関する二次形式で表される.
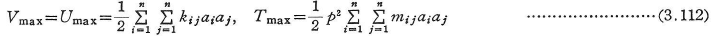
ここに,kijは剛性係数,mijは質量係数である.はりの曲げ振動の場合には,はりの曲げ剛性をEI,断面積をA,はりの単位体積質量をρとして次式のようになる.

プライムはxに関する微分を表す.
式(3.112)を式(3.110)に代入してp2が最小になるようにaiを決定する.そこで,p2をaiについて偏微分した式を零とおいて次式がえられる.
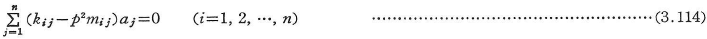
この同次連立一次方程式の係数行列式を零とおいた式を振動数方程式という.上記の固有値問題のm番目の固有値から第m次固有円振動数pmが求められる.また,pm2に対する固有ベクトルai(m)(i=1,2,…,n)を求めて式(3.111)に代入すれば,m次の固有振動モード![]() がえられる.
がえられる.
以上の方法をRayleigh-Ritzの方法という.この方法ではn個の固有振動数がえられるが,高次振動ほど誤差が大きいので,必要とする次数よりも式(3.111)の項数を多く用いるようにする.
骨組構造物のような複雑な連続体は,これを多自由度系に置換して上記の方法を適用すればよい.線形代数を用いてRayleigh-Ritz法を一般的に定式化したのがマトリックス構造解析法である.
3.6.2 マトリックス構造解析法
(a)振動数方程式
固有円振動数pで自由振動している骨組部材の平衡方程式は,減衰項を無視して次式のように表される.

ここに,d,fは部材端変位と部材端力の振動モードで,これらのベクトルの成分は静的解析の場合と同じである.kLは式(3.43)と同じ線形の剛性行列,mは質量マトリックスである.
式(3.115)を基準座標系に変換し,全部材について組み立てて境界条件の処理を行うと次式がえられる.
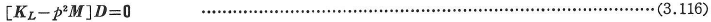
ここに,KLとMはそれぞれ構造物全体の線形の剛性行列と質量マトリックスである.この節点変位Dに関する同次連立一次方程式の係数行列式を零とおいて振動数方程式がえられる.
固有振動性状に及ぼす部材の軸方向力の影響を考慮する場合には,式(3.116)に幾何剛性行列(3.4.4参照)を加える.

ここで,KGに含まれている各部材の軸方向力の値は線形弾性解析により求めた値で,振動中は一定とする.
振動解析においては,連続体である部材の質量の取り扱い方に2通りの方法がある.ひとつは,分布質量による慣性力をエネルギー的に等価な節点の慣性力に置換する方法で,等価な質量マトリックスを整合質量マトリックス(consistent mass matrix)という.もう一つの方法は,部材の全質量を部材両端の節点に集中させる方法で,対角行列で表される集中質量マトリックス(lumped mass matrix)がえられる.なお,節点にある質量は,構造全体の質量マトリックスMを作成するときに直接Mに加算する.
(b)平面骨組構造
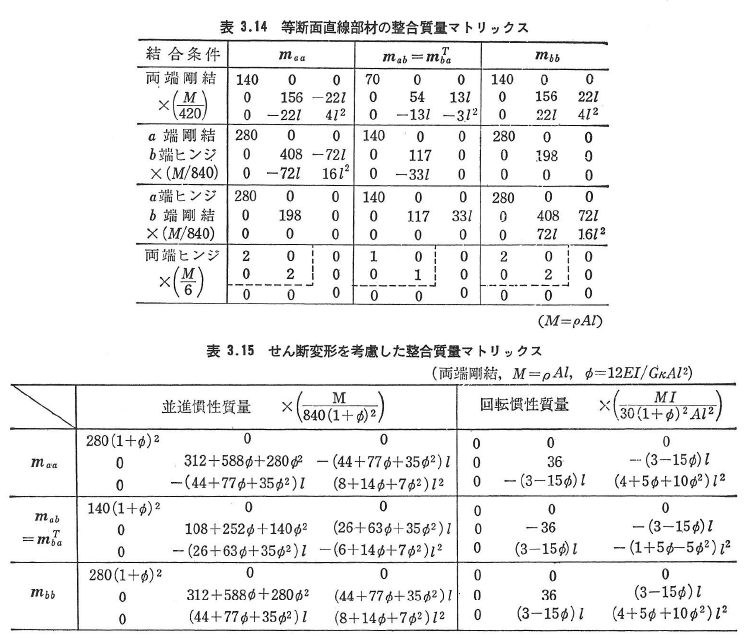
はり部材の整合質量マトリックスmを,表3.5と同じように小行列に分割して表3.14に示す.行列の各要素に1列目の係数を乗ずる.記号Mは部材の全質量である.
表3.14の質量マトリックスはせん断変形を無視した場合の並進慣性質量である.せん断変形の影響を考慮した場合の並進慣性と回転慣性による整合質量マトリックスを表3.15に示す.行列の各要素に1行目の係数を掛けるここに,Φは式(3.51)に示した値である.
部材の質量Mを両端に等分した集中質量マトリックスmは次式のような対角行列である.
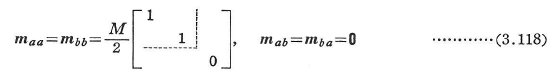
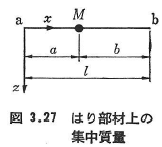
図3.27のようなはり部材上にある集中質量Mの並進慣性力による整合質量マトリックスは式(3.119)のようになる.
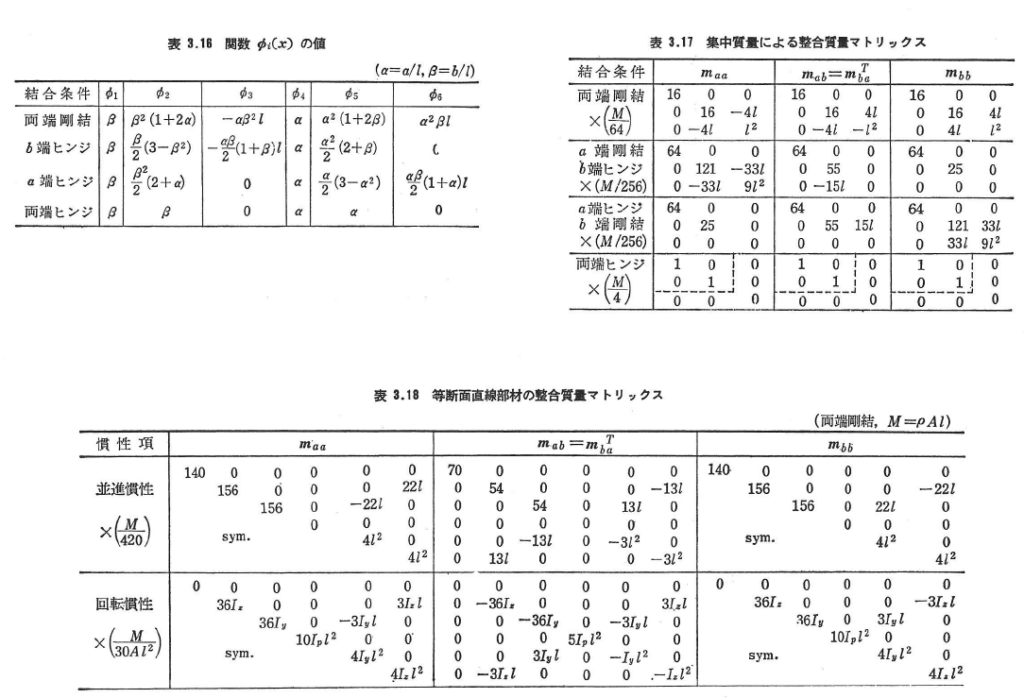
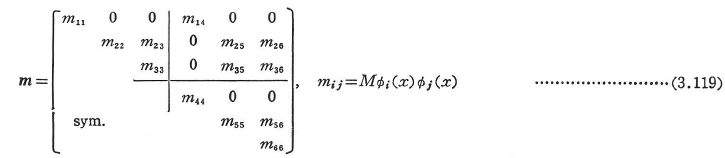
ここに,Φi,Φjは表3.16に示すMの位置xによる関数である.図3.12(b)のx-y平面内で解析する場合には,Φ3とΦ6の符号を逆にする.
部材の中央点(a=b=l/2)に集中質量Mがある場合の整合質量マトリックスは表3.17のようになる.
(c)立体骨組構造
両端で剛結合された一様な2軸対称断面の直線部材の整合質量マトリックスを表3.18に示す.ここに,Ipは極慣性モーメントである.
両端でヒンジ結合された部材では次式のようになる.
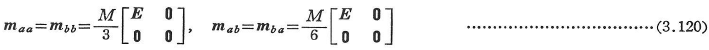
ここに,Eは三次の単位行列,0は三次の零行列である.
集中質量マトリックスは,式(3.120)においてmaa,mbbの係数をM/2にし,maa=mbb=0とする.
