Contents
3.3.1 エネルギー法
エネルギーに関する諸定理を用いた解析法を総称してエネルギー法という.線形弾性解析には,種々の定理を用いることができる.
(a)構造物の弾性変形
種々の荷重や支点移動により生ずる構造物の節点iの変位(または回転角)uiは,その点iに,uiの方向に単位仮想荷重![]() (または単位仮想モーメント
(または単位仮想モーメント![]() )を作用させたときに部材に蓄えられる補仮想ひずみエネルギー
)を作用させたときに部材に蓄えられる補仮想ひずみエネルギー![]() を用いて次式で求められる.
を用いて次式で求められる.
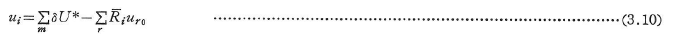
ここに,![]() は
は![]() (または
(または![]() )による支点反力,ur0は
)による支点反力,ur0は![]() 方向の支点移動量であり,
方向の支点移動量であり,![]() は全部材について,
は全部材について,![]() は全支点についての総和を表す.
は全支点についての総和を表す.
補仮想ひずみエネルギーδU*は,平面骨組構造物のはり部材とトラス部材について,それぞれ式(3.11),(3.12)で与えられる.
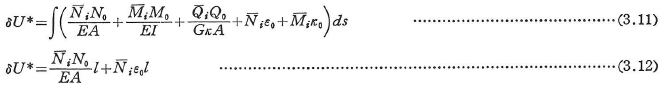
ここに,

ここに,

仮想荷重として,2点i,jにそれぞれ反対方向![]() に向く一対の単位仮想荷重
に向く一対の単位仮想荷重![]() と
と![]() を同時に作用させた場合には,式(3.10)のuiは
を同時に作用させた場合には,式(3.10)のuiは![]() 間の距離の変化になる.
間の距離の変化になる.
(b)不静定構造物の解法
n次内的・外的不静定構造物を応力法で解くために,n個の不静定力(不静定断面と反力)Xiを用いる.不静定力は次のn元連立一次方程式(弾性方程式)を解いて求められる.

ここに,ui0は荷重,温度変化や支点移動などによる静定基本形のXi方向の変位であり,仮想荷重として![]() =1を用いた場合の式(3.10)のuiに等しい.また,uijは静定基本形の変位の影響係数(
=1を用いた場合の式(3.10)のuiに等しい.また,uijは静定基本形の変位の影響係数(![]() =1によるXi方向の節点iの変位)であり,次式で求める.
=1によるXi方向の節点iの変位)であり,次式で求める.

δUij*は,はり部材とトラス部材について,式(3.17),(3.18)のようになる.

不静定構造物の断面力と反力は,次式で求められる.
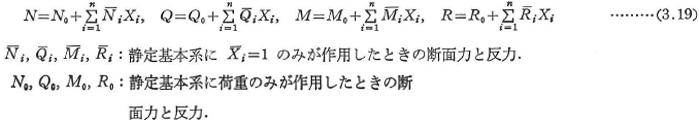
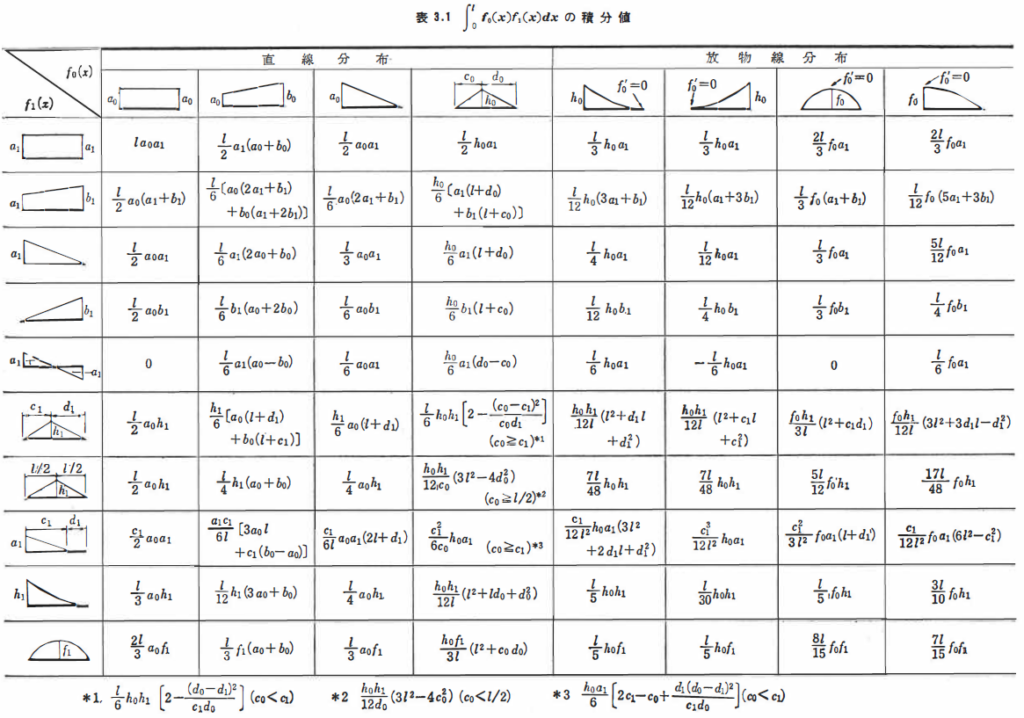
式(3.17)の積分演算には,表3.1を用いるとよい.
3.3.2 三連モーメント法と四連モーメント法
(a)三連モーメント法
図3.4(a)のような部材が連続して剛結された骨組構造において,節点iで剛結された2本の部材iとi+1を考える.部材iの長さをli,曲げ剛性をEliとし,荷重によりその両端はδi-1,δiだけ変位したものとする.
各剛節点において部材を切断し,その断面に図3.4(b)に示すような不静定モーメント(節点モーメント)Mi-1,Mi,Mi+1を作用させれば,剛節点iにおけるたわみ角の連続条件より次の三連モーメント式がえられる.
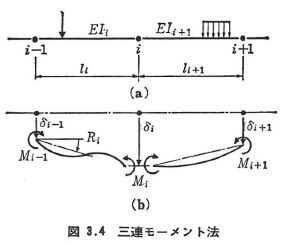
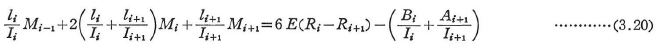
ここに,
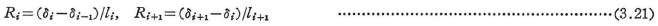
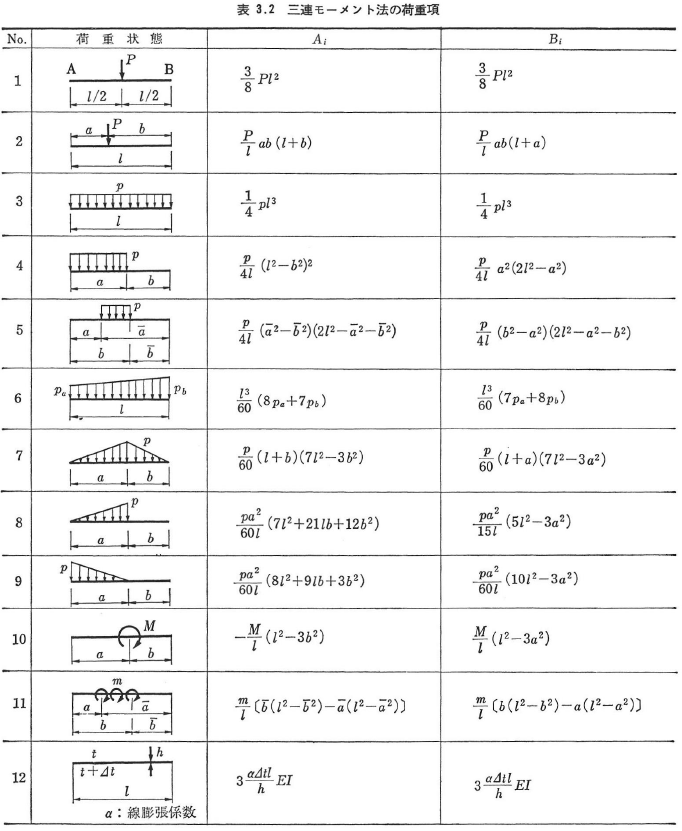
式(3.20)の右辺第2項は中間荷重項で,代表的な荷重によるAi,Biの値を表3.2に示す.
節点i-1が固定端の場合には,節点i-1において次式が成り立つ.

Riが未知の場合には,後述の角方程式(3.24)とせん断力のつり合い条件式(3.35)を用いる.
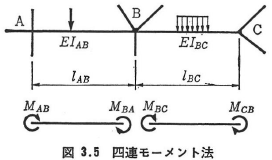
(b)四連モーメント法
図3.5のように,節点Bに3本以上の部材が剛結されている場合には四連モーメント法を用いる.図のように切断した2本の部材AB,BCについて,次の四連モーメント式が成り立つ.
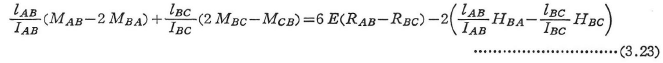
四連モーメント法では,力のつり合い条件式を機械的に求めるために,時計まわりを正とする材端モーメントを用いた,また右辺第2項の中間荷重項は式(3.20)と同じものであるが,表3.3のたわみ角法の荷重項で表した(式(3.32)参照).
節点Bにm本の部材が剛結されている場合には,これらの部材間の剛結条件を表すのに(m-1)個の式が成り立つ.材端モーメントを求めるためには,さらに力のつり合い条件式(節点方程式と層方程式)と角方程式を用いる.
(c)角方程式
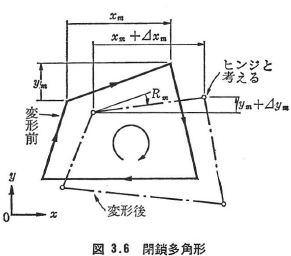
剛節構造物において,図3.6のような部材で囲まれた閉鎖多角形を考えると,多角形の変形に関して制約条件がある.この条件を部材回転角で表した式を角方程式といい,次式で表される.
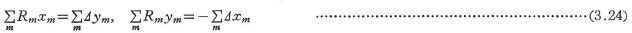
ここに,Rmは時計まわりを正とする部材回転角,xm,ymはそれぞれ部材のx,y座標軸への射影長であり,閉鎖多角形を時計まわりに一巡したときの向きを各部材軸の正の方向としたとき,xm,ymの方向がそれぞれx,y座標軸の方向と一致する場合を正,逆向きの場合を負とする.Δxm,Δymは変形後の部材長の変化(伸び)のx,y座標軸への射影長である.![]() は1つの閉鎖形を形成する部材についての総和を表す.
は1つの閉鎖形を形成する部材についての総和を表す.
ラーメン構造の分析では,通常部材長の変化を無視するので,式(3.24)の右辺を零におくことができる.ただし,温度変化や支点移動がある場合には,このときの長さの変化をΔxm,Δymで表したものを用いる.
式(3.24)を剛節構造物のすべての閉鎖形についてたてれば,構造物全体の変形に関する部材回転角の適合条件式がえられる.したがって,独立な部材回転角の個数nは,全部材数から閉鎖形の数の2倍を引いた数になる.
従属な部材回転角Rmは,独立部材回転角に選ばれた角Rkによって次式で与えられる.

ここに,ψmkはRk=1とし,他の独立部材回転角をすべて0にしたときの部材mの回転角である.
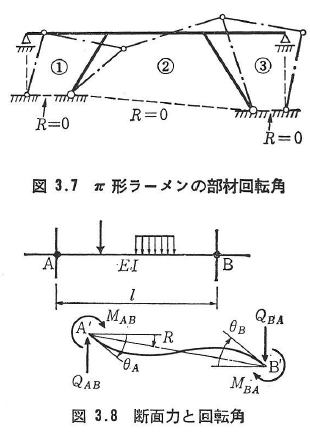
図3.7のような5本の部材(実線)で構成されたπ形ラーメンを考える.はりの両端の可動支点を考慮して,2個の仮想ヒンジ支点と5本の剛な仮想部材(破線)を加えると,3個の閉鎖形ができる.柱脚のヒンジ支点の移動がない場合には,支点を結ぶ3本の仮想部材の回転角は0であるから,独立な部材回転角の数は7-2×3=1個である.
3.3.3 たわみ角法
(a)たわみ角公式
図3.8のように剛節構造物から部材ABを取り出すと,A,B端に作用する材端モーメントMAB,MBAと節点回転角θA,θB,部材回転角Rの関係は次式で表される.
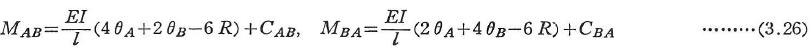
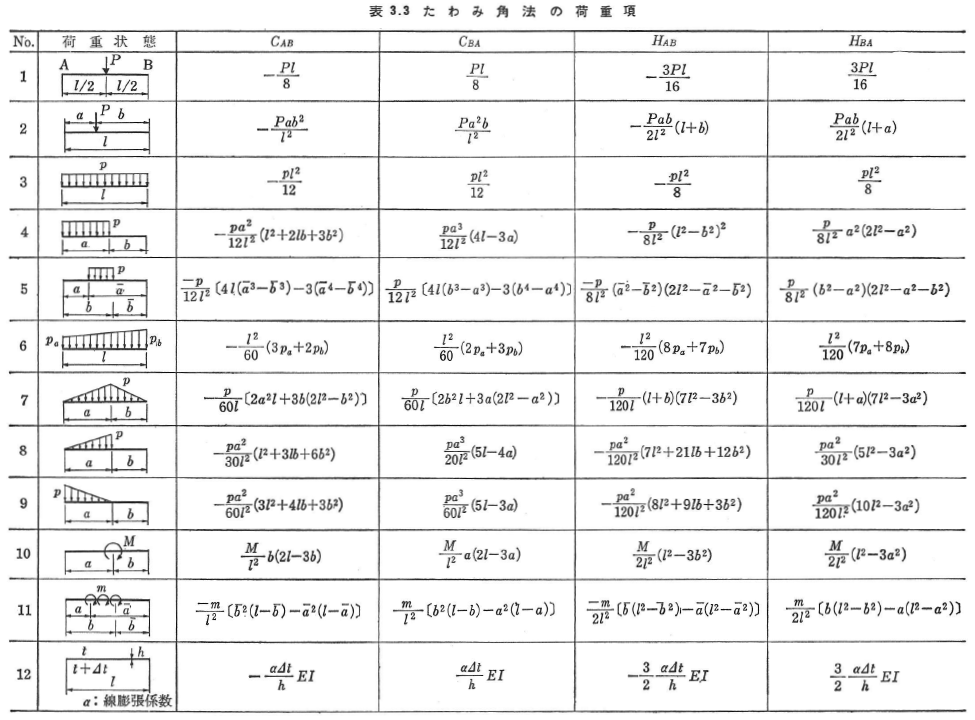
ここに,CAB,CBAは両端固定ばりの材端モーメントであり,たわみ角法の荷重項という.
式(3.26)を次式のように変形することができる.
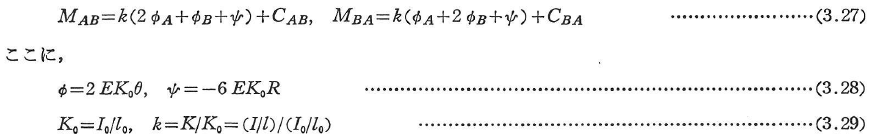
K0は基準剛度,Kは部材剛度,kは部材の剛比である.式(3.27)をたわみ角法の一般公式という.
部材端の境界条件に応じて,以下の公式が導かれる.
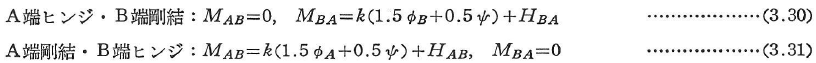
固定端の場合には,式(3.27)において固定端の節点回転角Φを0とおく.HAB,HBA中間荷重による荷重項で,CAB,CBAの値とともに表3.3に示す.これらの荷重項と表3.2の荷重項との間には次の関係がある.
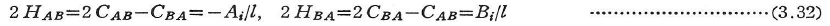
(b)節点方程式と層方程式
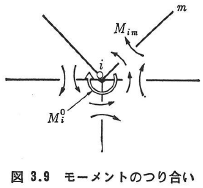
節点iに着目し,これに剛結された部材の材端モーメントMimと節点iに作用する外力モーメントMi0とのつり合い条件は,図3.9より次式で表される.
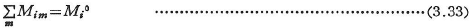
これを節点方程式という.
次に,図3.8の材端せん断力は次式で与えられる.
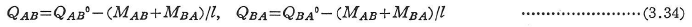
ここに,QAB0,QBA0はそれぞれ部材ABを単純ばりと考えたときに部材上の中間荷重によるA端とB端のせん断力である.
図3.10に示すラーメンについて,切断面t1–t1におけるせん断力のつり合い条件式は次式のようになる.
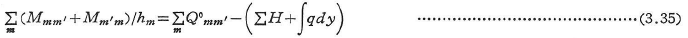
ここに,hmはせん断された柱mm‘の長さであり,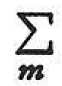 はt1–t1切断面で切断された柱についての総和である.右辺第2項は,t1–t1切断面より上の部分に作用する水平荷重の総和である.荷重がすべて鉛直方向に作用する場合には,式(3.35)の右辺は0になる.
はt1–t1切断面で切断された柱についての総和である.右辺第2項は,t1–t1切断面より上の部分に作用する水平荷重の総和である.荷重がすべて鉛直方向に作用する場合には,式(3.35)の右辺は0になる.
式(3.35)を層方程式といい,図3.10のラーメンではさらに切断面t2–t2,t3–t3,t4–t4において層方程式をたてる.たわみ角法では,節点回転角θと部材回転角R(またはΦとψ)の未知量と同じ数だけの力のつり合い条件式がえられる.
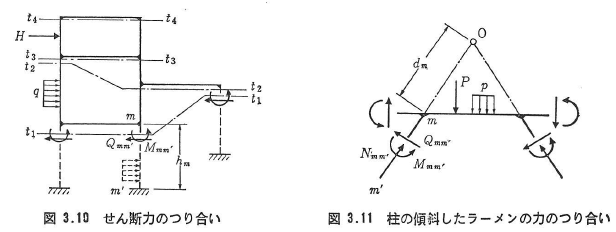
柱が傾斜している異形ラーメンでは,式(3.35)の層方程式を用いることができない.
図3.7のπ型ラーメンの場合には,図3.11のように切断された部分について,点Oまわりのモーメントのつり合い条件から,式(3.34)を用いて次式がえられる.
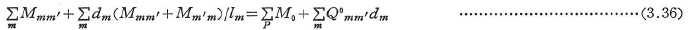
ここに,dmは材端せん断力Qmm‘の作用線から点Oまでの距離であり, は切断された部材についての総和を表す.また,右辺第1項は,外力P,pによる点Oまわりのモーメントである.
は切断された部材についての総和を表す.また,右辺第1項は,外力P,pによる点Oまわりのモーメントである.
3.3.4 モーメント分配法
モーメント分配法は,ハーディ-クロス(Hardy-Cross)が提案した剛節構造物の解法で,固定モーメント法ともいう.この解法は図上計算法であって,まず節点をすべて固定して各節点の不均衡モーメントを計算し,次に各節点の固定を順次解除して不均衡モーメントが零に収束するまで繰り返し計算を図上で行う.解法手順は以下のようになる.
- 全剛節点の回転を固定し,各部材ごとに表3.3の固定端モーメントCim(またはHim)を求める.
- 節点iの固定モーメント(拘束モーメントともいう)
 を求める.
を求める.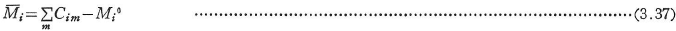
ここに,Mi0は節点iに作用する外力モーメントであり,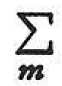 は節点iに剛結された部材についての総和を表す.
は節点iに剛結された部材についての総和を表す. - 節点iの拘束を解除するために,他の節点を拘束したままで,節点iに不均衡モーメント ー
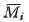 を作用させる. ー
を作用させる. ー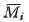 は,節点iに剛結された部材の剛比kimに比例して配分され,部材ijの分配モーメント
は,節点iに剛結された部材の剛比kimに比例して配分され,部材ijの分配モーメント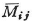 は次式で求められる.ここに,μijは分配率である.
は次式で求められる.ここに,μijは分配率である.
- 分配モーメント
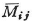 は,他端の節点jに伝達される.これを到達モーメントΔMijといい,伝達率νijを用いて求められる.
は,他端の節点jに伝達される.これを到達モーメントΔMijといい,伝達率νijを用いて求められる.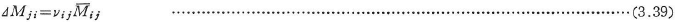
- 節点jに到達したモーメントを集計し,その逆まわりのモーメントを不均衡モーメントとして節点jに作用させて拘束を解除する.このとき,他のすべての節点は固定したままである.1回目の解除のときには,式(3.37)の
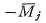 を不均衡モーメントに加える.
を不均衡モーメントに加える. - 全節点の不均衡モーメントが零に収束するまで③~⑤の計算を繰り返す.最後に,各部材の材端モーメントMijを次式で計算する.

ここに,kは反復回数である.なお,ヒンジ端にはモーメントは伝達されない.また,固定端ではモーメントを解放する必要はない.
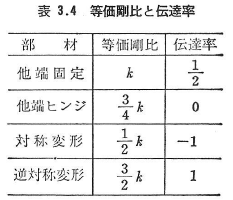
一端ヒンジの部材や対称変形または逆対称変形する部材では,分配率の計算において部材の剛比kの代わりに等価剛比を用いて,剛結の場合と同じように扱う.等断面の場合の等価剛比と伝達率を表3.4に示す.
以上の解法は節点変位のない場合の計算法であり,節点が移動する場合には計算が複雑になる.
3.3.5 マトリックス構造解析法
マトリックス構造解析法は式を組み立てるのに座標変換の手法を用いるので,複雑な任意の形状の構造物の解析に適用することができ,平面解析でも同じ計算手順を用いる.ここでは,非線形解析にも拡張が容易で,より汎用性のある変位法(直接剛性法)について説明する.
(a)平衡方程式
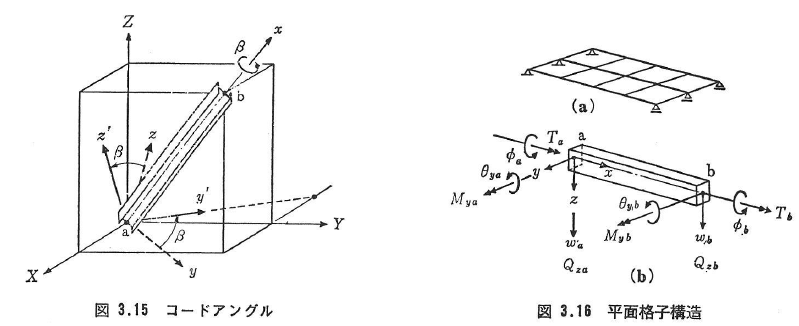
部材は等断面直線材とする.部材の一端aを原点とし,x軸は部材中心軸に,y,z軸は断面主軸にそれぞれ一致する右手直行直線座標系(x,y,z)を部材座標(局所座標ともいう)に選ぶ.部材の両端a,bの座標軸方向の並進変位u,v,wと座標軸に関して右ねじまわりの回転角Φ,θy,θzを,a端とb端についてそれぞれ六次の列ベクトルで表す.
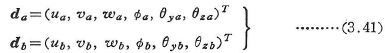
ここに,Φはねじり角であり,微小変位理論ではθy=-dw/dx,θz=dv/dxである.Tは転置記号である.
式(3.41)の変位の方向の部材端力を次式で表す.
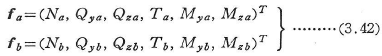
ここに,Nは軸力,TはSt. Venantのねじりモーメント,QとMはy,z軸に関するせん断力と曲げモーメントである.図3.12は以上の成分をx-y平面に分けて示したものである.
部材の平衡方程式(剛性方程式)は,次の行列式で与えられる.
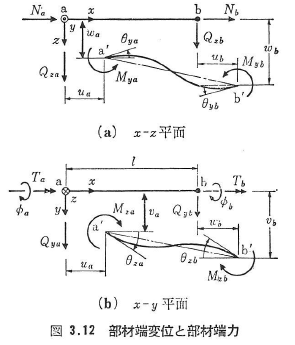

ここに,係数行列は部材の剛性行列であり,fa0,fb0は中間荷重によるa,b端の等価節点力ベクトルである.
構造物全体に共通な1つの基準座標(全体座標ともいう)として,適当な位置に原点をもつ右手直行直線座標系(X,Y,Z)を定める.(x,y,z)座標を(X,Y,Z)座標に変換する後述の座標変換行列Tを用いて,式(3.43)を次式のように変換する.
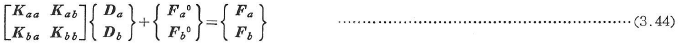
ここに,T-1=TTを考慮して
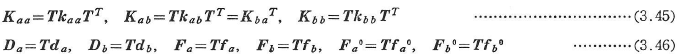
節点iの節点変位をDi,節点荷重(または反力)をPiとする.各節点において変位の適合条件と力のつり合い条件から部材端変位Da,Dbと部材端力Fa,Fbを消去すると,式(3.44)を全部材について組み立てた次式の構造全体の平衡方程式がえられる.

ここに,Fi0は節点iに集まる部材の中間荷重項Fa0またはFb0の和である.各小行列とベクトルの次数は節点の自由度数(平面骨組は3,立体骨組では6)に等しい.なお,nは節点の総数である.
式(3.47)の係数行列KLは構造物全体の剛性行列であり,その小行列Kijは次のようにして求められる.
対角小行列Kiiは節点iに集まる部材のiに結合された部材端側の剛性行列KabまたはKbbの和になる.上三角行列部分のKij(i<j)は,節点iとjをつなぐ部材の剛性行列Kabに等しい.ただし,部材のa端(原点)側の節点番号がb端側の節点番号より小さくなるように部材座標の原点を定めたものとする.もし,i,jをつなぐ部材がなければKij=0である.
式(3.47)には境界条件が与えられていないので,行列KLは特異行列で一意的な解をもたない.そこで,境界条件を一般的に考えて,節点移動がある場合について説明する.
いま,第2節点にΔ2が与えられたものとするとD2=Δ2で,P2には節点移動に必要な未知の強制力Q2が含まれる.このときには,節点2に関する平衡方程式は式(3.47)と独立になるのでこの式を分離し,式(3.47)を次式のように変形する.

ここに,Eは単位行列,0は零行列で,剛性行列の2行目と2列目の小行列は対角小行列以外すべて0とする.式(3.48)を解けばD2=Δ2と他の節点変位が求められる.この解を次式に代入してQ2がえられる.

さて,境界条件の処理は,節点2が固定支点のときにはΔ2=0とおけば式(3.48)はそのまま成り立つ.また,節点2の反力R2は式(3.49)でQ2=R2として求められる.可動支点やヒンジ支点の場合には,拘束された変位成分に対応する行と列について上記の操作を行う.なお,式(3.48)で意味のない2列目と2行目の式を抜いて行列を縮小してもよいが,電子計算機を使用する場合には,通常は縮小しない.また,反力や強制力は,部材端力を求めた後で節点の力のつり合い条件から求め,式(3.49)を用いない.部材端力を求めるには,式(3.46)によってDiをdaまたはdbに逆変換し,これらを式(3.43)に代入してfa,fbを求める.
(b)平面骨組構造
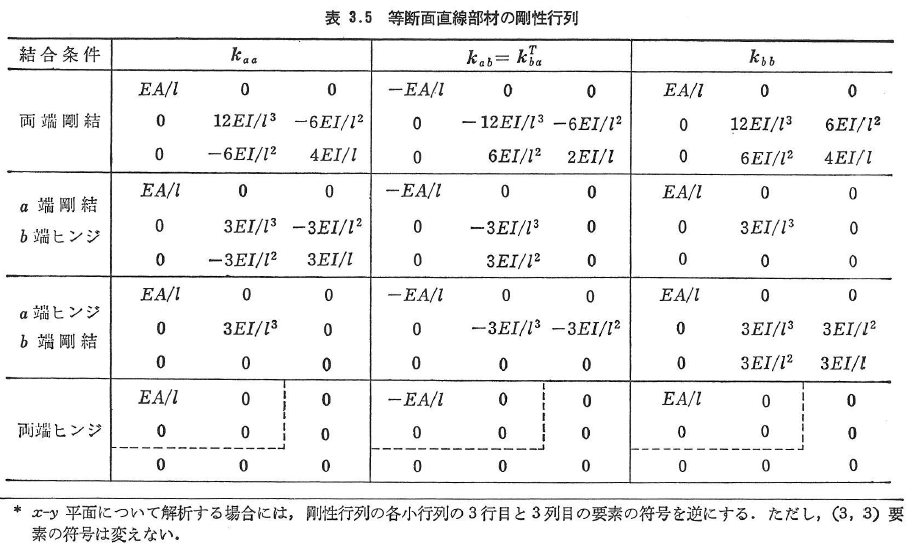
平面解析では,図3.12(a)のx-z平面を考えて,式(3.42)を次式のように縮小する.
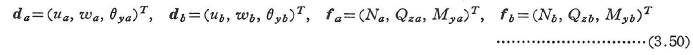
式(3.43)の部材の剛性行列を表3.5に示す*.ヒンジ支点た可動支点で支持された部材では,この部材端を剛結点とみなし,境界条件の処理によって支点における結合条件を考慮する.また,自由端も剛結点とみなして特別の処理は行わない.両端ヒンジの剛性行列は,合成ラーメンにおけるトラス部材に使用し,平面トラスの解析では破線の(2×2)行列に縮小した剛性行列を用いる.
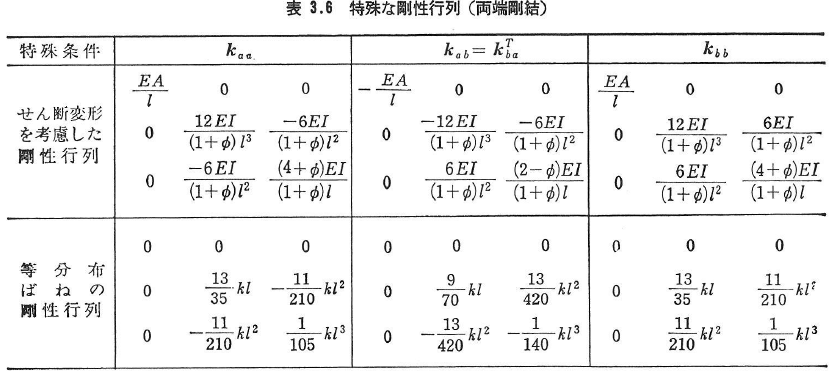
次に,せん断変形を考慮した場合の剛性行列を表3.6に示す.表中の記号Φは,せん断力の補正係数kを用いて次式で与えられる.

図3.13に示すx軸方向に一様に分布するばねで支持されたはり部材の剛性行列は,表3.5の剛性行列に,表3.6のばねによる剛性行列を加えたものである.ここに,kは単位長さ当たりのばね定数(N/m/m)である.なお,ばねの剛性行列は近似式であり,kl2/EI≪1程度の誤差を含む.
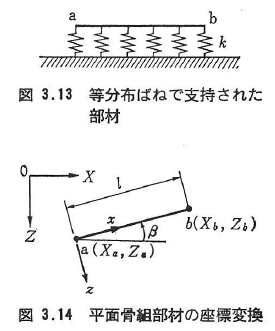
座標変換行列Tは,図3.14の座標値を用いて次式のようになる.
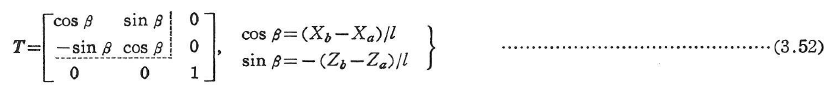
平面トラスの解析では,Tを(2×2)の大きさに縮小する.
式(3.48)の荷重項Piは,節点iに作用する集中荷重のX,Z成分と外力モーメントである.
式(3.43)の部材上に作用する荷重による中間荷重項fa0,fb0を次式のように表す.
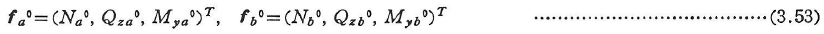
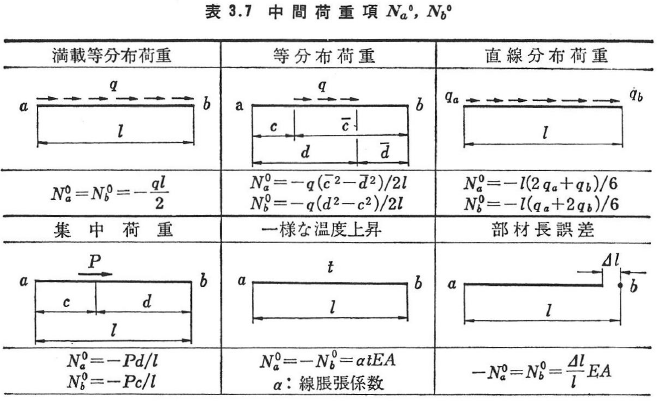
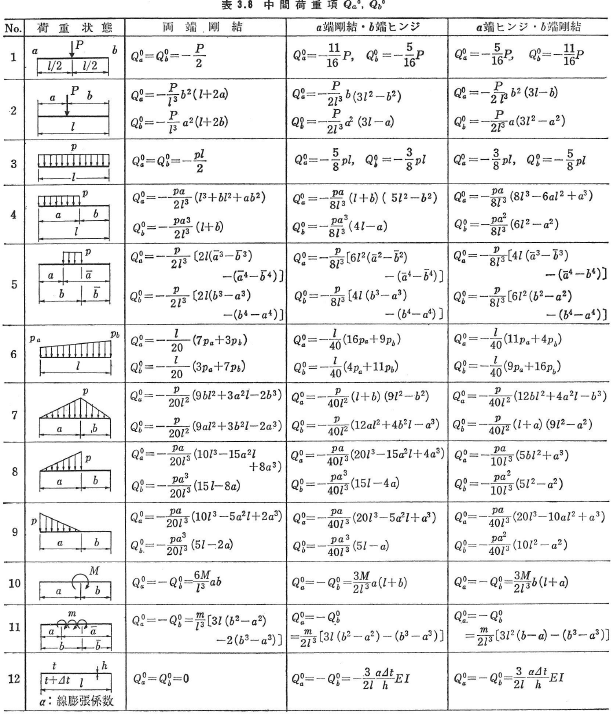
x軸方向に作用する中間荷重に対してQz0,My0はa,b端ともに零であり,Na0,Nb0は表3.7のようになる.z軸方向の荷重に対してはNa0=Nb0=0で,Qza0,Qzb0は部材を固定ばりと考えたときのa,b端の反力の逆向き(z軸方向が正)の値である.これらの値を,他の結合条件の場合とともに表3.8に示す.Mya0,Myb0は,それぞれ表3.3のCAB,CBA(またはHAB,HBA)の符号を逆にした値に等しい.ヒンジ支点または可動支点で支持された部材では,支点を剛結点と考えた場合の荷重項を用いて,剛性行列と同じように境界条件の処理によりヒンジ端を考慮することができる.
(c)立体骨組構造
両端で剛結された等断面直線部材の剛性行列は次式のようになる.
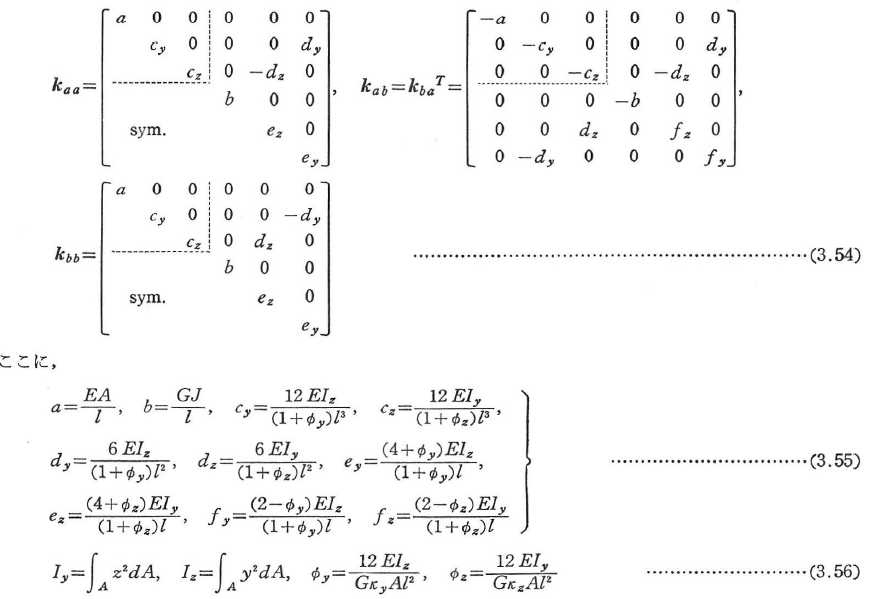
ここで,Φy=Φz=0とおけば,せん断変形を無視した場合の剛性行列がえられる.立体行列の剛性行列は,(1,1)要素以外の要素を0とおいて,式(3.54)の核剛性行列を(3×3)に縮小したものである.なお,Jはサンブナンのねじり定数である.
座標変換行列Tを(3×3)の小行列T0に分割して次式のように表す.
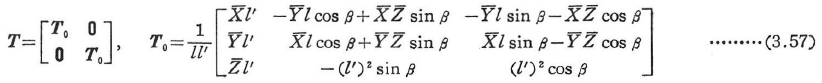
ここに,(Xa,Ya,Za),(Xb,Yb,Zb)を両端a,bの基準座標に関する座標値をとれば,
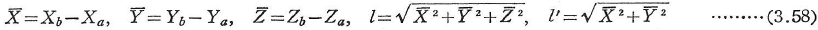
また,βはコードアングル(chord angle)とよばれる次のような回転角である.
図3.15において,部材abをx軸まわりに角度βだけ右ねじの方向に回転して,主軸yをX-Y平面上にのるようにしたときの角度である.ただし,回転後のz’軸の正の方向がZ座標値の増大する方向に向かうまで回転する.
x軸がZ軸と平行な場合には,l’=0になるので式(3.57)の代わりに次式を用いる.
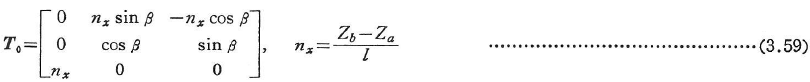
ここに,βはx軸を右ねじの方向に回転して,y軸をY軸に一致させたときの角度であり,nxは±1のいずれかの値である.
トラス部材では,y,z軸の方向は任意であるので,式(3.57)の第1列(x軸の方向余弦)だけを用いて他の要素を0とする.
(d)平面格子構造
図3.16(a)のような平面格子構造では,節点の自由度数は3になる.そこで,図3.16(b)のように座標軸を定めて,部材端の変位と断面力を次式のようにおく.
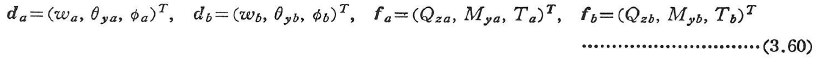
部材の剛性行列は,式(3.55),(3.56)の記号を用いて次のようになる.
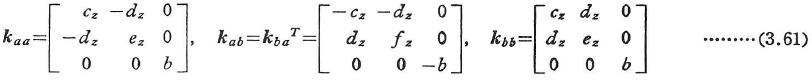
座標変換行列は,図3.17の角度βを用いて,
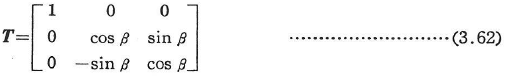
曲げねじり変形を考慮する場合には,各節点においてねじれ率Φ’(=dΦ/dx)と曲げねじりモーメントMω,全ねじりモーメントTxを考慮して,式(3.60)の代わりに次のベクトルを用いる.
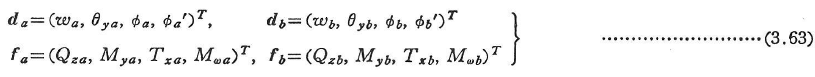
二軸対称断面部材の剛性行列は次のようになる.
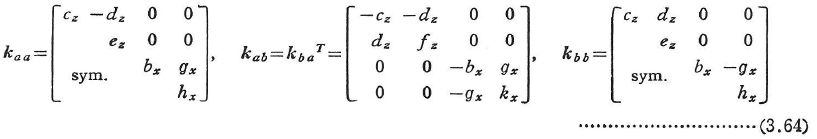
ここに,曲げねじり剛性EIωを用いて,
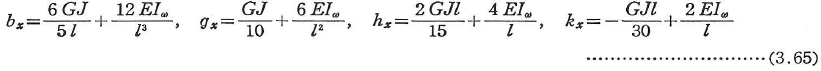
座標変換行列には次式を用いる.

3.3.6 影響線
構造物の点kに単位集中荷重Pk=1を作用させたときの着目点iの変位(または支点rの反力や部材軸上の点mの断面力)の値δik(またはRrk,Smk)を影響係数という.また,荷重の位置kにδik(またはRrk,Smk)の値をプロットし,Pkを順次移動して描いた線図を影響線または影響線図という.影響線は荷重位置の関数であり,これを用いて移動荷重による変位や反力などの最大値を求めることができるが,単位荷重を用いていることと,分布移動荷重に対しては重ね合わせの原理を用いることから,非線形性が表れる構造物には原則として適用できない.
変位(またはたわみ角)の影響線は,相反作用の定理を用いると,点iに単位集中荷重Pi=1(または単位モーメントMi=1)を作用させたときの弾性曲線δki(またはθki)が点iの単位荷重方向の変位(またはたわみ角)の影響線δik(またはθik)になる.
不静定構造物における不静定力の影響線は,ミューラー-ブレスロウ(Muller-Breslau)の定理により容易に求められる.すなわち,構造物のある点iの不静定力(反力,断面力)XiのPk=1による影響線Xikは,Xiのみを解放した構造物を考えて,その点iにXiに逆向きの単位集中荷重![]() =1を作用させたときのPk方向の変位の弾性曲線
=1を作用させたときのPk方向の変位の弾性曲線![]() を,
を,![]() 方向の変位(
方向の変位(![]() がモーメントであればたわみ角)
がモーメントであればたわみ角)![]() で割った値に等しい.
で割った値に等しい.
高次不静定構造物では,式(3.15)の右辺のui0に![]() =1による静定基本系のXi方向の変位
=1による静定基本系のXi方向の変位![]() を用いた方程式の解Xikが,Pk=1による不静定力Xiの影響係数になる.点mの断面力の影響係数Smkは,静定基本系の影響係数Smk0を求め,式(3.19)と同じように重ね合わせの原理により次式で求められる.
を用いた方程式の解Xikが,Pk=1による不静定力Xiの影響係数になる.点mの断面力の影響係数Smkは,静定基本系の影響係数Smk0を求め,式(3.19)と同じように重ね合わせの原理により次式で求められる.

