3.4.1　線形座屈解析

　線形座屈解析法は，構造物に起きる分岐座屈の問題（3.2.5参照）において，図3.18に示す分岐荷重（座屈荷重）P_crと分岐方向の変形様式（座屈モード）Δu_cを求めるための簡略化された解法である．

　線形座屈解析では，通常次の仮定を用いている．

1. 座屈前に生じるu₀は小さくて，座屈前の形状変化による影響は無視する．
2. 分岐点に達するまでの構造物の弾性挙動は線形で，応力は荷重に比例する．
3. 分岐点における力のつり合いは座屈変形後の形状で考えるが，この時の変位Δu_cは微小（無限小）とするので，Δu_cに関して線形化することができる．

　以上のように，線形座屈解析では微小変位を仮定しているので，分岐後の応力や変位を求めることはできない．また，座屈前の変形が大きい場合や不安定分岐座屈が起きる場合（図3.3(a)の曲線B）には，線形座屈解析によって求められた座屈荷重は実際の構造物の座屈荷重よりかなり大きくなることがある．

　骨組構造物のような多自由度系の解析では，まず線形弾性解析により与えられた荷重P₀による部材の断面力f₀を求める．P₀をλ倍したときに座屈するものとすれば，分岐点での各部材の断面力fは，仮定２により構造物について1個の無次元パラメーター（荷重倍数）λを用いて，f=λf₀と表すことができる．

　次に，このfを初期応力と考えて分岐点での平衡条件式を求めると，分岐点では荷重が増加することなく別なつり合い状態Δu_cが存在することから，仮定３を考慮してΔu_cに関する同次連立一次方程式がえられる．

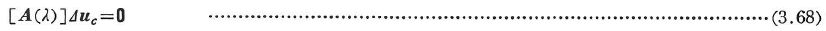
ここに，Aは構造物の剛性と荷重状態によって定まる行列で，マトリックス構造解析法では剛性行列とよんでいる．

　式（3.68）より，Δu_c≠0なる解が存在する（分岐座屈が起きる）ための条件として，次の条件式がえられる．

　このλに関する行列A(λ)の固有値問題を解いて最小の固有値λ_crを求めれば，座屈荷重P_crはP_cr＝λ_crP₀となる．また，座屈モードΔu_cはλ_crに対する固有ベクトルで与えられる．なお，解法により，式（3.68）は標準的な線形固有値問題にならないことがある（3.4.3(d)参照）．

3.4.2　エネルギー法

　線形座屈解析では，分岐点Cをポテンシャルの基準点に選び，座屈変形による全ポテンシャルエネルギーの変化ΔΠ_cを用いる．座屈変形Δu_cによる分岐点からのひずみエネルギーと外力ポテンシャルの変化をそれぞれΔU_c，ΔH_cとすると，中立の平衡条件は次式で表される．

　真直な柱に中心軸圧縮力Pが作用するときの曲げ座屈問題を考えると，柱のたわみvが座屈変形であるので，柱の曲げ剛性をEI，柱の長さをlとしてΔU_c，ΔH_cは，

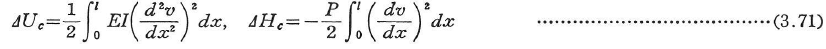
で与えられる．これらを式（3.70）に代入すると，

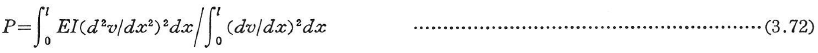
　この式はv(x)を固有関数とするレイリー（Rayleigh）商である．vに近似関数を用いるとRayleigh商の積極的性質により，vの精度よりもはるかに精度のよい近似座屈荷重P_crが求められるが，その値は常に真の座屈荷重より大きくなる．

　エネルギー法では，座屈モードΔu_cを仮定した近似解法を用いることが多い．いま，１自由度系を考えてΔu_cを座標xの関数とすると，幾何学的境界条件を満たす一次独立な関数Φ_i(x)と未定係数a_iを用いて，Δu_cを次の関数列で近似する．

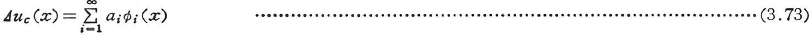
　式（3.73）を適当な項数nで打ち切り，これを式（3.72）のvに代入する．Pの最小値を求めるために，∂P/∂a_i=0(i=1,2,・・・，n)とおくとa_iに関するn元の同次連立一次方程式がえられるから，a_i≠0の条件よりこの固有値問題を解いて座屈荷重が求められる．この方法をリッツ（Ritz）またはRayleigh-Ritzの方法という．式（3.73）のΔu_cをΔΠ_cに用いて，a_iによるΔΠ_cの第一変分を零とおいても同じ結果がえられる．

　関数Φ_i(x)にはxの多項式や三角関数を用いることが多いが，Φ_i(x)がさらに力学的境界条件を満たす場合にはRitzの方法よりも計算が簡単になり，精度もよくなる．この方法をガレルキン（Galerkin）法という．

　次に，エネルギー原理による座屈判定基準を調べてみる．柱の曲げ座屈問題を例にとれば，式（3.73）を式（3.71）に代入したものを式（3.70）に用いると，ΔΠ_cはベクトルa=(a₁,a₂,・・・,a_n)^Tの二次形式で表される．

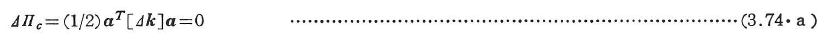
ここに，Δkはn次の対称行列で，その要素Δk_ijは次式で与えられる．なお，’はxに関する微分を表す．

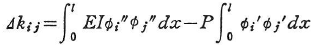
　式（3.74・a）における独立変数はaであることに注意して，aによるΔΠ_cの第一変分と第二変分を求めると，式（3.4），（3.8）から次の各式がえられる．

　a≠0より，式（3.74）の各式はΔkが特異行列であることを示しており，座屈判定基準としてどの式を用いても同じ結果がえられることがわかる．なお，式（3.74・b）はPを固有値とする標準的な固有値問題である．

　レイリー-リッツ（Rayleigh-Ritz）の方法を骨組構造物の座屈解析に適用する際には，式（3.73）のΔu_cを各部材ごとに仮定する．このとき，aとして式（3.41）の部材端変位を用いた解法がマトリックス構造解析法（変位法）である．

3.4.3　三連・四連モーメント法とたわみ角法

（a）座屈たわみ角公式

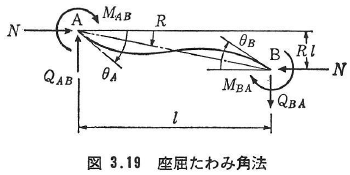
ここに，圧縮力Nを正として，

軸方向力Nが引張力のときにはNを正として，

N=0のときには，α=1/3，β=1/6になる．

　式（3.75）をM_AB，M_BAについて解くと次式がえられる．

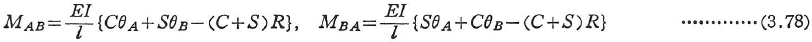
ここに，C，Sは安定関数とよばれるものであり，式（3.76）のα，βを用いて次式で与えられる．

　式（3.78）を座屈たわみ角公式という．N=0のときにはC=4，S=2となり，通常のたわみ角公式（3.26）に一致する．一端がヒンジの場合には，式（3.78）は次のようになる．

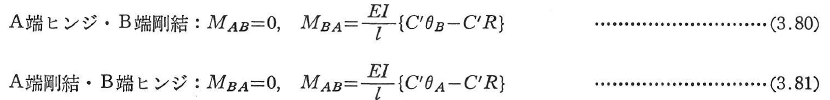
　ここに，

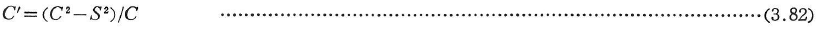
安定関数を表3.9に示す．

（b）三連・四連モーメント法

図3.5の剛節点Bにおけるたわみ角の剛結条件に式（3.75）を用いると，座屈四連モーメント式がえられる．

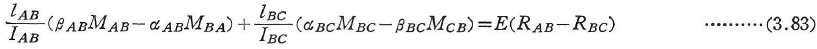
三連モーメント法では，図3.4に示した節点モーメントM_iを用いると，次の公式がえられる．

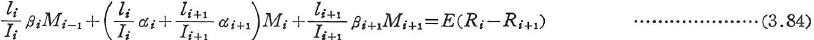
（c）節点方程式と層方程式

　線形座屈解析では，与えられた荷重に対する平衡状態から外力が変化することなく微小な座屈変形が生じる新たな平衡状態を求める．したがって，力のつり合い条件には荷重を考慮しない．

　節点方程式は，式（3.33）においてM_i⁰とおいて，

　層方程式を導くときには座屈変形を考慮するが，変位は微小として線形化する．図3.19に示した部材のモーメントのつり合いより材端せん断力Q_AB，Q_BAが求められる．

　図3.10のラーメンの切断面t₁–t₁の層方程式は，式（3.86）を用いると次式のようになる．

ここに，は切断した部材についての総和，は軸方向力が生じた部材についての総和で両端ピンの柱も含める．なお，N_tは圧縮力を正とする．

　柱が平行でない異形ラーメンでは，式（3.87）の層方程式を用いることができないので，これに代わる式を求める．

　剛節点をすべてヒンジ節点に置換し，これに微小な仮想回転角δRを加える．この仮想変形は，独立部材回転角（3.3.2(c)参照）のなかの1つをδR_kとし，他の独立部材回転角をすべて零にした変形を考える．この変形で生じる従属部材回転角δR_mは，式（3.25）より次のようになる．

　仮想変位δRによって変形したヒンジ構造は平衡状態を保っているので，材端モーメントと軸方向力による仮想仕事の総和は零になる．したがって，次式が成り立つ．

　これに式（3.88）を代入すると，δR_kは任意の独立量であるから次の平衡方程式がえられる．

ここに，は部材回転角が生じる部材についての総和，は軸方向力の生じる部材についての総和である．なお，ψ_kk=1とする．式（3.89）は，独立部材回転角の数だけ成り立つ．

（d）座屈条件式

　たわみ角法では，式（3.25）（3.78）を式（3.85）と式（3.87）または式（3.89）に代入すると，θ_iとR_kに関する同次連立一次方程式がえられるから，その係数行列の行列式を零とおいた式が座屈条件式である．

　この行列には各部材の軸方向力Nが含まれているので，3.4.1で説明したパラメーターλを用いるとλに関する式（3.68）の固有値問題になるが，λは安定関数の中に含まれているために標準的な固有値問題の解法を適用することができない．

　四連モーメント法では，式（3.83）と式（3.87）または式（3.89）を連立させた式に式（3.25），（3.85）を用いると，M_mm‘とR_kに関する同次連立一次方程式が求められる．この場合にも，座屈条件式はλに関する超越方程式になる．

3.4.4　マトリックス構造解析法

（a）座屈条件式

　部材端変位dと部材端力fに線形弾性解析（3.3.5）の場合と同じベクトルを用いると，座屈変形が生じたときの部材の平衡方程式は次のようになる．

ここに，k_Lは線形の剛性行列で，式（3.43）の係数行列と同じ行列である．k_Gは幾何剛性行列または初期応力マトリックスとよばれ，座屈前に生じて応力に依存する．λは，3.4.1で説明したパラメーターである．

　式（3.90）を座標変換して全部材について集めると，構造物全体の平衡方程式として，次式のλを固有値，全節点変位Dを固有値ベクトルとする固有値問題がえられる．

ここに，K_Gは初期応力が生じた部材のk_Gを座標変換して組み立てた行列である．

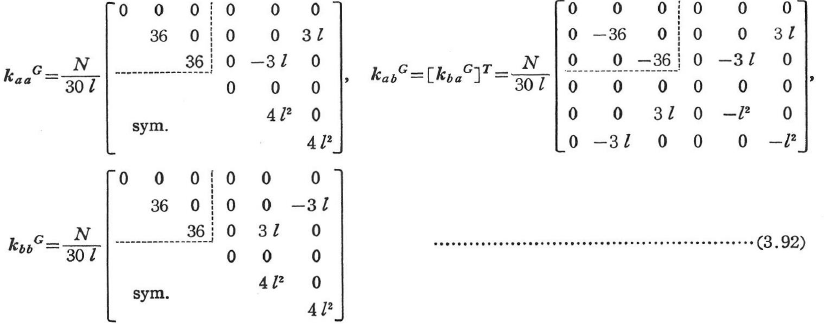
　以下に骨組構造物の曲げ座屈を考えて，初期応力として軸方向力N（引張力を正とする）のみを考慮した幾何剛性行列を示す．この行列は安定関数C，Sをkについて級数展開したときの第2項（第1項はk_L）に相当し，打切り誤差はk²(=Nl²/EI)のオーダーで真の値よりも大きい座屈荷重がえられる．

（b）平面骨組構造

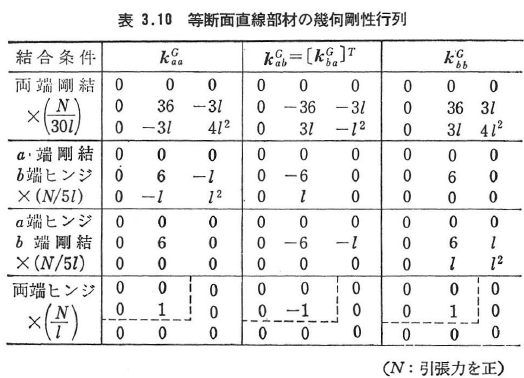
　式（3.90）の幾何剛性行列k_Gを，表3.5に対応した形で表3.10に示す．各行列の要素には1列目の係数がかかる．

（c）立体骨組構造

　両端で剛結された等断面直線部材の幾何剛性行列を次に示す．トラス材ではk_aa^G，k_bb^Gの（2,2）と（3,3）要素をN/l，k_ab^Gでは-N/lとして，各行列を（3×3）に縮小する．