これまでに扱ったラーメンや連続ばりは,温度変化による部材の伸縮や沈下などによる視点変位がない限り,節点は変位せず,部材角Rは生じない.例えば,図8.14に示すような2部材のラーメンの場合,点Aを中心に半径ACで描いた弧aa’と点Bを中心に半径BCで描いた弧bb’の交点は一点Cに定まる.すなわち,点Cは変位しないことがわかる.一方,図8.15に示す門形ラーメンの場合,点Bは点Aを中心に半径ABの弧bb’上を動くことができ,点Cは点Dを中心にして半径DCで描いた弧cc’上を動くことができるから,BC間の距離を部材長lに保ったままで,点B,Cは図に示す点B1,C1の位置に移動が可能である.
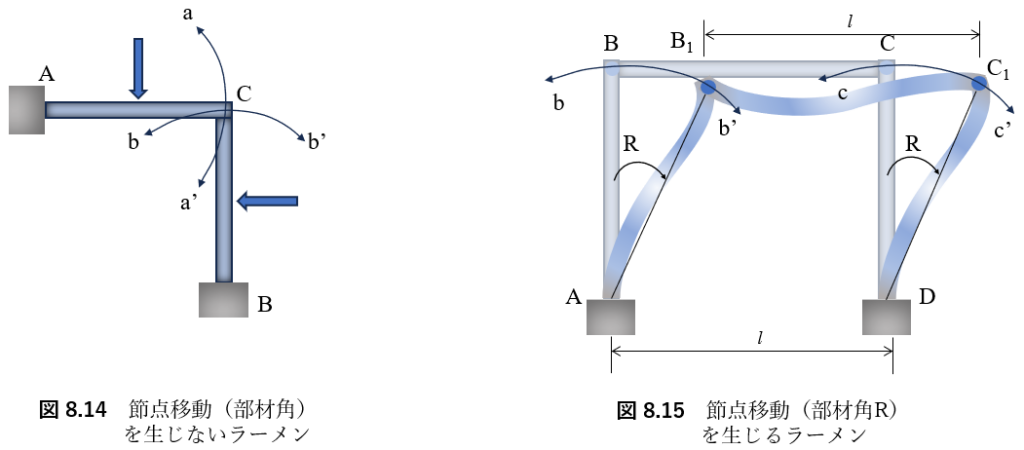
この結果,部材ABとDCに部材角Rが生じることになる.ラーメンを解くときには,このように節点移動が生じるかどうかを判別し,節点移動が生じる場合は,部材角Rが未知数に加わる.一つの構造物について,それぞれの部材角の間には,満足すべき幾何学的関係(変形条件)がある.ここでは,通常取り扱うことの多い,長方形ラーメンについて部材角の性質をまとめておこう.部材長の変化を無視し,温度変化,支点変位がないとすれば,長方形ラーメンについて次のことがいえる.
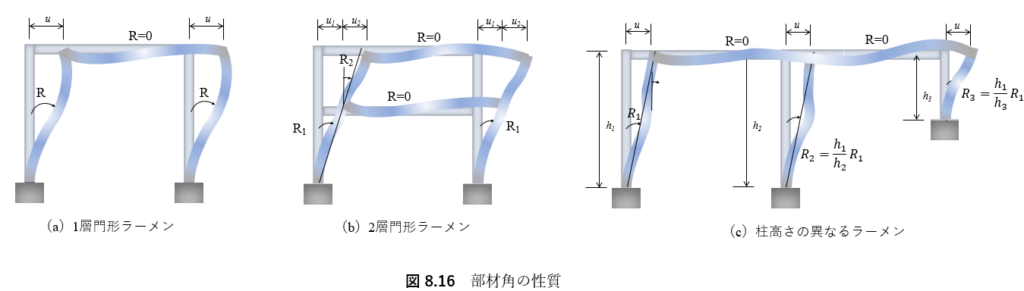
- 水平なはりの部材角はつねにゼロである.
- 一般に,垂直な柱は部材角を生じる.
- 一つの層に属する柱のたわみはすべて等しい.したがって,柱の高さが一定ならば,部材角はすべて等しい(図8.16(a),(b)参照).
- 一つの矩形ラーメンでは,未知数Rの数は層の数と一致する.
- 柱の高さが違っても,部材角は柱の高さの比で決定できるので,同じ層内の未知数Rの数は変わらない(図(c)参照).