たわみ角法は，部材の変形，すなわち，たわみ角法を未知数とする連立方程式をたてて，不静定構造物を解く変形法の一つで，公式は簡単で記憶しやすく，不静定次数の高いラーメンや連続ばりを解くための優れた方法である．ここでは，まず用語の定義と符号の約束について述べる．

➡️（1）端モーメント
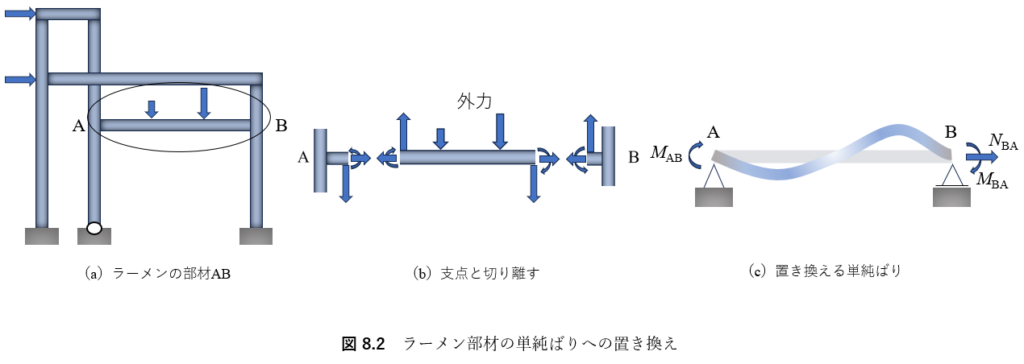
　図8.2(a)に示すラーメンを構成するある部材ABを図(b)のように切り出して考えると，その両端は，それぞれに軸力，せん断力，曲げモーメントの三つの応力を受けている．この6個の応力のうち，３個を与えれば，残りの3個は，3個のつり合い条件より求めることができる．すなわち，切り出した部材ABは図(c)に示すように，両端に曲げモーメントを，ローラー端に軸力を外力として受ける単純ばりに置き換えて考えることができる．この両方の部材端に作用する曲げモーメントのことを材端モーメント，略して端モーメントという．以後，部材ABのＡ端に作用する曲げモーメントをＭ_ABと表し，部材ABのＢ端に作用する曲げモーメントをＭ_BAと表す．端モーメントの符号は，両端とも，時計まわりを正とする．

➡️（2）接線角
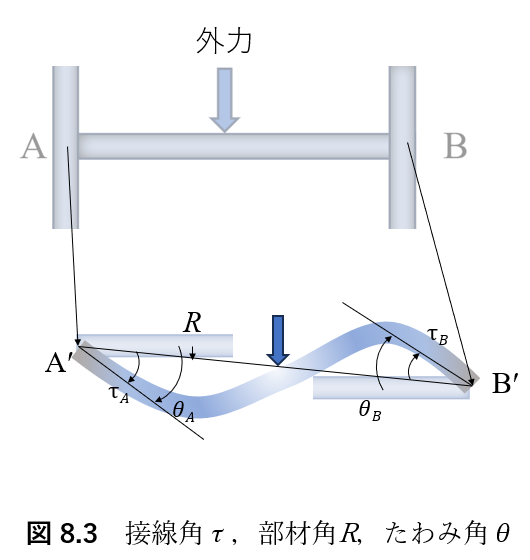
　図8.3に示すように，変形した部材の両端において，部材軸に引いた接線と部材の両端を結ぶ直線のなす角を接線角という．記号にはτを用い，A端の接線角をτ_A，B端の接線角をτ_Bと書く．端モーメントの符号は，接線の回転が時計まわりのとき，正とする．接線角は，公式の誘導の途中に用いるが，最終的な未治療としては用いない．

➡️（3）部材角
　図8.3に示すように，部材ABが変位を起こしてA’B’の位置に移ったとき，部材の両端を結ぶ直線のA’B’と変形前の軸線ABのなす角を部材角といい，記号Rで表す．端モーメントの符号は，時計まわりに回転したときを正とする．

➡️（4）たわみ角
　図8.3に示すように，部材ABが変形しつつ変位してA’B’に移動したとき，変位後の部材両端における接線が，変位・変形前の部材軸となす角をたわみ角という．記号にはθを用い，Ａ端のたわみ角をθ_A，B端のたわみ角をθ_Bと書き，時計まわりを正とする．定義と図8.3より明らかなように，たわみ角は接線角と部材角の和であるから，次式が成り立つ．

また，当然ながら，部材角Rがゼロのとき，たわみ角と接線角は等しい．