Contents
3.2.1 構造解析の基本式
骨組構造物に生じる反力,部材力,変位は次の3つの基本式を用いて求められる.
①力のつり合い条件式,②力と変位の関係式,③変位の適合条件式
①は,構造物全体についての力のつり合い条件式(3.1)もしくは,構造物を切断したときに切断面,節点,部材や部分構造物に作用する内力(断面力)と外力との間で成り立つ条件式である.
②は,部材両端の材端力と材端変位の関係などを断面諸量と材料定数を用いて表した式である.
③は変位の連続条件を表す式であり,部材の接合点や切断面における変位の連続条件などに用いる.
3.2.2 応力法と変位法
静的構造物の反力と応力は①の力のつり合い条件式のみで求められるが,不静定構造物では弾性変形を考慮して反力や応力が求められるので,3つの基本式のすべてを用いる必要がある.不静定構造物の解法は応力法と変位法に大別され,最終的に解く連立方程式の未知変数が応力の場合を応力法といい,変位の場合を変位法(または変形法)という.また,未知変数として応力と変位を混用した混合法が用いられることもある.
応力法では,構造物の不静定次数に等しい数だけの反力または断面力を未知変数に選ぶ.不静定構造物から,この未知反力に対する変位の拘束を解放し,また断面力に対しては構造物を切断して断面力を解放する.このようにして得られた構造物を静定基本系といい,解放された反力または断面力を不静定力という.
不静定力は静定基本系に対して未知の外力であるが,これを単位にとれば単位荷重による静定基本系の変位を求めることができる.そこで,不静定力と荷重による変位を求め,不静定力の作用点での変位の適合条件に用いると不静定力のみを未知量とする連立一次方程式(これを弾性方程式という)を導くことができる.この方程式を解いて不静定力を求めれば,不静定構造物の任意の点の応力や変位は,荷重と不静定力による静定基本系の応力や変位の重ね合わせで求められる.
応力法には,三連・四連モーメント法や最小仕事の原理などの補エネルギーに関する定理を用いた解法がある.変位法としてたわみ角法がよく知られており,近年ではマトリックス変位法が用いられる.
応力法は不静定力の選び方に人為的な判断を要するので,高次不静定構造物の解析では式の作成が煩雑になる.一方,変位法は方程式の作成を機械的に行うことができる.特に,マトリックス変位法は構造物の形状によらず式を統一的に組み立てることができる長所があり,さらに種々の非線形解析に適用しやすいので,電子計算機を利用する場合に適した解法である.
3.2.3 線形弾性問題
線形弾性解析では,次の仮定を用いる.
- 構造材料は弾性体であって,Hookeの法則が成り立つ.
- 構造物の変形は微小で,変形による影響は無視できる(微小変位の仮定).
この2つの仮定が成り立つ線形弾性問題では,構造物の応力や変位は荷重に比例し,重ね合わせの原理を適用することができる.
仮定1が成り立たない問題では応力とひずみが比例しない.これを材料非線形問題という.仮定2に基づく解析理論を微小変位理論といい,この仮定が成り立たない問題を幾何学的非線形問題という.また,両方の非線形性が現れる問題を複合非線形問題という.
これらの仮定のほかに,問題を単純化して計算を容易にするために,構造解析では種々の仮定を用いる.骨組構造解析では,部材の断面について,形状不変の仮定と平面保持の仮定(ベルヌーイ-オイラー(Bernoulli-Euler)の仮定ともいう)が重要である.
3.2.4 非線形問題
(a)材料非線形性
構造物に生じる応力が弾性限界を越えて塑性変形が生じる場合には,構造材料の応力-ひずみ曲線を考慮した非線形解析が必要になる.また,弾性限界であっても応力とひずみが比例しない材料では,非線形問題となる.
部材の一部に塑性変形が生じた後の変位や応力は弾塑性解析によって求められる.この解析では,降伏条件式を用いて塑性域を判定し,増分理論に基づく逐次計算により解を求める.また,構造物の耐荷力(塑性崩壊荷重)を簡便に求める方法として塑性解析法が用いられる.この解析法では,はり部材に生じる塑性域は断面内に集約して生じるものと仮定し,塑性ヒンジの概念を用いて単純化された曲げモーメント-曲率の関係を用いる.このために,崩壊荷重に達した後の構造物の挙動を求めることができない.
塑性材料のほかに粘性材料による非線形問題がある.粘性体では応力とひずみが比例せず,荷重が一定であってもひずみが時間の経過とともに増大するクリープ現象が現れる.また,弾性と粘性の両特性を備えたプラスチックなどの粘弾性体も時間に依存する特性を示す.このような時間依存性のある材料の非線形問題は,時間に関する増分計算の手法を用いて解析する.
(b)幾何学的非線形解析
微小変位の仮定が成立しない場合にはひずみ-変位関係式は非線形になり,力のつり合い条件と変位の適合条件を変形後の状態で求められなければならない.このような幾何学的非線形問題の解析には有限変位理論を用いる.
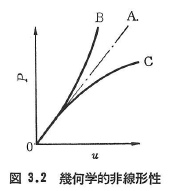
図3.2は,幾何学的非線形性が現れる構造物の変位uと荷重Pの関係を示したものである.線形応答関係Aに対して,Bは同じ大きさの荷重に対して変位が小さくなる場合であり,Cは逆に大きくなる場合である.Bのような非線形性は,部材の軸方向引張力の大きい吊橋などに現れ,Cの非線形性は軸方向圧縮力の大きいアーチなどに現れる.
3.2.5 弾性安定問題
(a)不安定現象
骨組構造物や薄肉構造物のように,部材の大きさを示す寸法のうち,少なくとも1つの寸法が他の寸法に比べて非常に小さい場合には,荷重がある値に達すると変形が急激に増大する不安定現象が生じることがある.この現象は主として幾何学的非線形性に起因するものであり,この種の問題を弾性安定問題という.
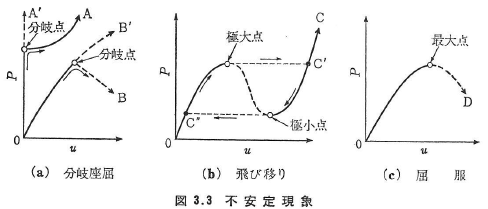
不安定現象には3つの形式があり,これを荷重-変位曲線で示すと図3.3のようになる.ここに,実線は安定な平衡状態を表し,破線は不安定な平衡状態を示す.また,○印は両者の境界点で中立な平衡状態を示す.
図3.3(a)は荷重が○印の値(座屈荷重)に達すると,突然にそれまでの変形とは異なるまったく別な変形の平衡状態に移る現象で,分岐座屈または通常,座屈とよんでいる.つり合い曲線Aは,柱などにみられる座屈現象で分岐後は安定な平衡状態に移る.Bは分岐後の平衡状態が不安定な場合であり,アーチなどに起きる現象である.
図3.3(b)では荷重が増加して極大点に達するとC’点に飛び移って安定な平衡状態を保つ.また,荷重を減少させると極小点からC”点に飛び移る.このような現象が飛び移りといい,偏平なアーチやシェルに起きる.
図3.3(c)は薄肉パイプを曲げたときや,構造物の弾塑性挙動で一般的にみられる不安定現象で屈服という.荷重が最大点に達するとそれ以後の平衡状態は不安定となり,構造物は崩壊する.
実際の構造物では分岐座屈と飛び移りの両方が起きる場合もあり,材料非線形性も現れてさらに複雑な挙動を示す.
(b)エネルギーによる判定
構造物の平衡状態の安定.不安定や中立の条件をエネルギー原理により調べることができる.いま,保存力場を考えて,全ポテンシャルエネルギーを![]() とする.n個の自由度ui(i=1,2,…,n)をもつ構造系において,与えられた荷重に対して構造物が平衡状態にあれば,全ポテンシャルエネルギー停留の原理により次式が成り立つ.
とする.n個の自由度ui(i=1,2,…,n)をもつ構造系において,与えられた荷重に対して構造物が平衡状態にあれば,全ポテンシャルエネルギー停留の原理により次式が成り立つ.
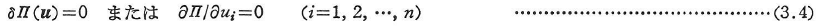
ここに,![]() はuによる
はuによる![]() の第1変分である.
の第1変分である.
線形弾性問題では,![]() はuiの二次式になるので,式(3.4)はuiに関する一次式であり,したがって平衡状態は1つしか存在しない.これをキルヒホップ(Kirchhoff)の解の唯一性定理という.しかし,有限変位理論により求めた
はuiの二次式になるので,式(3.4)はuiに関する一次式であり,したがって平衡状態は1つしか存在しない.これをキルヒホップ(Kirchhoff)の解の唯一性定理という.しかし,有限変位理論により求めた![]() にはuiに関する高次項が含まれているので,荷重条件によって式(3.4)は2組以上の解をもつようになる.このn元連立非線形方程式(3.4)を種々の荷重段階で解いて,図3.2,3.3の平衡曲線が求められる.
にはuiに関する高次項が含まれているので,荷重条件によって式(3.4)は2組以上の解をもつようになる.このn元連立非線形方程式(3.4)を種々の荷重段階で解いて,図3.2,3.3の平衡曲線が求められる.
次に,平衡状態にある構造物の安定は,この平衡状態uから任意の微小変位δuを与えたときの![]() の変化(
の変化(![]() の増分)
の増分)![]() の符号によって調べることができる.すなわち,
の符号によって調べることができる.すなわち,

とすれば,
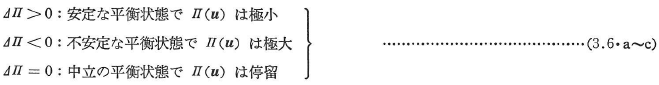
ここで,![]() をuの近傍で級数展開すれば,
をuの近傍で級数展開すれば,

となるから,これに式(3.4)を用いて,![]() 以上の高次の項を省略すれば,式(3.6)において,
以上の高次の項を省略すれば,式(3.6)において,![]() の代わりに
の代わりに![]() の第二変分
の第二変分![]() を用いることができる.したがって,
を用いることができる.したがって,![]() ≦0のときに種々の不安定現象が起きることがわかる.このとき,不安定現象を
≦0のときに種々の不安定現象が起きることがわかる.このとき,不安定現象を![]() の符号,
の符号,![]() =0ならば
=0ならば![]() の符号によって分類することができる.
の符号によって分類することができる.![]() =0を書き換えると,
=0を書き換えると,
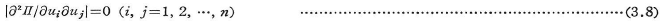
これを行列表示して次式がえられる.

不安定現象が起きる中立点を求めるためには,式(3.9)にuが含まれているので,式(3.4)と(3.9)を連立させて解かなければならい.これに対し,線形座屈解析法では,線形化の手法により式(3.4)と式(3.9)は独立な式になるので,式(3.9)の固有値問題を解いて座屈荷重を求めることができる.
