Contents
2.3.1 基本事項
細長い棒材が重心軸に垂直に作用する力のみを受け,部材には主として曲げモーメントが作用するときこの部材をはりという.図2.22は重心軸が直線で,断面の主軸の方向が全長にわたって不変のはり,すなわち直線ばりが右ねじの法則に従うベクトルMで表される曲げモーメントを受けている場合を示す.一様断面の直線ばりが純曲げを受けるときは,せん断力は働かず,①重心軸は伸縮せず,たわみ曲線は一平面内の円弧となる.②すべての横断面は変形後も平面を保持し,重心軸との直交性を保つことが分かっている.さらに,③材料はHookeの法則に従い,引張・圧縮に対する弾性係数の値は等しい.④軸方向に走っているはりの繊維は他の繊維とは独立に伸縮し,その間にはせん断応力は働かないし横方向に圧力も生じないと仮定する.
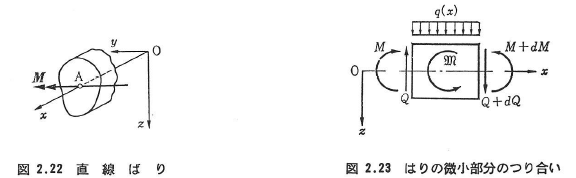
図2.23は,はりの微小部分の図であるが,曲げモーメントM,せん断力Qと分布荷重qの関係は,この部分に働く外力集中モーメント![]() が0のとき,dx→0にとれば,
が0のとき,dx→0にとれば,

となるが,![]() の作用する点の近傍ではQの分布形は変化しない(
の作用する点の近傍ではQの分布形は変化しない(![]() は例えば横ばりよりのねじりモーメントの伝達によって生じる).符号に関しては,通常,はりの下側に引張を生じる曲げモーメントMを正,せん断力QについてはdQがzの正方向に向いているとき正とする.
は例えば横ばりよりのねじりモーメントの伝達によって生じる).符号に関しては,通常,はりの下側に引張を生じる曲げモーメントMを正,せん断力QについてはdQがzの正方向に向いているとき正とする.
2.3.2 真直ばりの単純曲げによる応力
図2.22において,y,z軸を断面の2つの主軸にとり,y軸まわり曲げモーメントMyとz軸の正方向に凸の曲率xあるいは,曲率半径ρを用いて曲げ応力σxを引張を正として表せば,
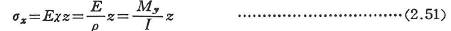
となる.ここに,Iは点Aを通りy軸に平行な軸のまわりの断面二次モーメントであり,表2.1には各種断面のIが与えられている.この関係は,断面が緩やかに変化していたり,分布あるいは集中横方向力によるせん断力が存在する場合にもほぼ十分な精度で成立する場合が多く,単純曲げ理論といわれる.
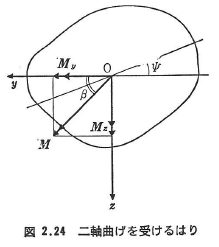
さて,図2.24のようにMがy軸の方向と角度βをなすとき,中立軸がy軸と![]() の角度をなすならば,
の角度をなすならば,
となる.ただし,A,Iyy,Izz,Iyzは,それぞれ断面積,y軸とz軸まわりの断面二次モーメント,断面相乗モーメントである.
y,z軸が断面の二主軸と一致する場合は,

2.3.3 真直ばりの曲げモーメントと軸力による応力
2.2.1にあるように,座標軸を図2.15のようにとり,軸力をN(引張を正),y軸,z軸を断面の重心を通るように選べば,

ただし,
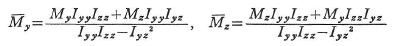
2.3.4 曲げによるせん断応力
図2.25には充実断面と薄肉断面の近似的なせん断応力分布ふが示されている.図にあるような一様なせん断応力の大きさをτとすれば,一軸曲げの場合,τは両断面ともに同じように次式で表すことができる.

ここに,Q,G,I,tは,それぞれ垂直せん断力,斜線を施した部分の中立軸まわりの断面一次モーメント,はりの中立軸に関する断面二次モーメント,そして断面厚である.
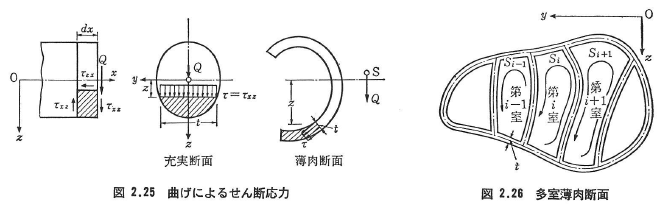
図2.26には多室薄肉断面が示されているが,この場合,式(2.58)は単に静定せん断応力を与えるに過ぎない.いま,![]() を静定せん断流とすれば,2方向の曲げがかかった場合,式(2.58)は
を静定せん断流とすれば,2方向の曲げがかかった場合,式(2.58)は

となる.ただし,
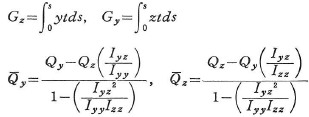
ここに,Qy,Qzは,それぞれy軸,z軸方向のせん断力である.
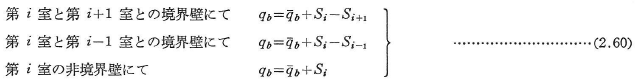
であり,Siは次のひずみエネルギー,

がSiに関して極小値をとることから次式で求められる.

ただし,
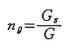
ここに,Gsはある基準材料,例えば鋼のせん断弾性係数である.したがって,n室の薄肉断面の不静定せん断流は次式より求められる.
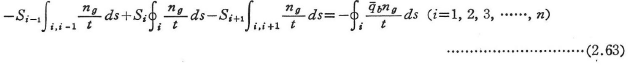
ここに,![]() は第i室とi-1室との境界壁に沿っての積分を表している.
は第i室とi-1室との境界壁に沿っての積分を表している.
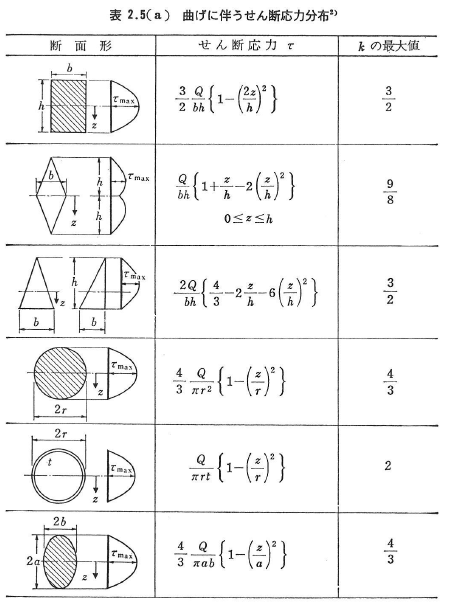
表2.5(a)には代表的な断面のせん断応力分布が示されている.
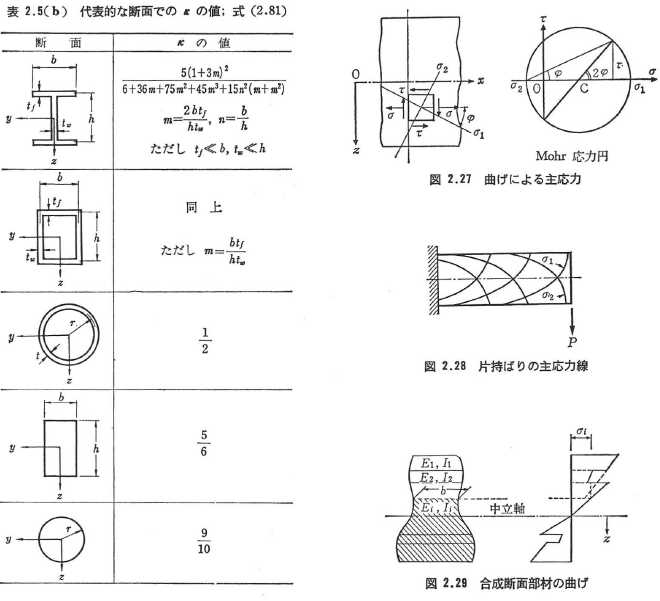
2.3.5 曲げによる主応力
図2.27にははりの一部分が示されているが,曲げ応力σは式(2.51)より,また,せん断応力τは式(2.58)より与えられるから,Mohrの応力円により,最大主応力σ1と最小主応力σ2は,
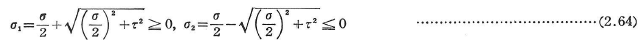
主応力の方向は図2.27を参照して,反時計方向のφを正とするとき,

で与えられる.
2組の直交曲線で,その曲線上の各点の接線がこの点の最大,最小主応力の方向に一致するとき,この曲線を主応力線という.
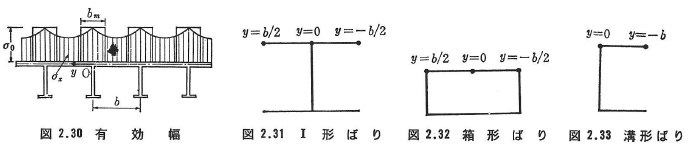
図2.28には片持ばりの主応力線が示されている.
2.3.6 合成断面部材の応力
弾性定数の異なる2種類以上の材料を軸方向にずれないように接合して作られたはりを合成ばりという.はりの直ひずみは断面内で連続で直線分布すると考え,第i部の弾性係数と中立軸まわりの断面二次モーメントをそれぞれEi,Iiとすれば,曲率x,曲げ応力σi,せん断力τiは図2.29を参照して,

ここに,M,Q,y,b,Gは,それぞれ曲げモーメント,せん断力,中立軸より垂直距離,τiを求めている断面内の点での断面厚,そしてハッチした部分の中立軸まわりの断面一次モーメントである.
2.3.7 せん断遅れと有効幅
比較的薄い平板に補強材,あるいは縦桁などが結合されている場合に平板は,全体をはりと見なしたときのフランジと考えられる.曲げモーメントがこのはりに作用するときには,軸方向応力σはフランジが中立軸に平行であるにもかかわらず一様な分布とはならず,補強材などとの結合点ではσの値は大きくなる.この現象をせん断遅れという.この場合には問題を簡単にするため,結合点でのσの大きさをもった一様な応力が実際の応力分布と等価となるようにある特定の幅にわたって作用するものと考えれば便利である.この板幅のことを弾性的有効幅という.
有効幅は二次元弾性問題としてAiryの応力関数を用い,また面内変位をそれによって表現することにより面内応力を求めれば得ることができる.Airyの応力関数については前章を参照されたい.
z軸を平板の横断面方向にとり,図2.30のように,y=0を等間隔に配置された補剛材との結合点,実際の板幅をb,板厚を一定としたときは,有効幅bmは次式で定義できる.

ただし,σ0はy=0でのσx–νσyの値,もしくはσxの値である.以下,前者の場合はbmはbm‘,後者の場合はbmとして区別することにする.
例として![]() なる曲げモーメントが作用した場合を考える.これはAiryの応力関数のフーリエ級数の一項を与えられるが,一項のみをとれば有効幅は以下のように軸方向に一定となる.
なる曲げモーメントが作用した場合を考える.これはAiryの応力関数のフーリエ級数の一項を与えられるが,一項のみをとれば有効幅は以下のように軸方向に一定となる.
- 等間隔bでリブが配置されているとき,図2.30において境界条件として結合点ではy方向の変位が0であるとすれば,
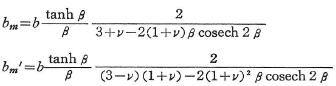
ただし,
- T形あるいはI形ばりのとき,図2.31のように,結合点をy=0にとれば,境界条件としてy=0のときy方向の変位が0,y=±b/2で,σy=0,τxy=0と考えると,β=λb/2として,
- 箱形ばりのとき,図2.32のように,フランジ中央点をy=0にとり,境界条件をy=±b/2でσy=0と考えればβ=λb/2として,

- 溝形ばりのとき,図2.33のように結合点をy=0にとるとき,境界条件はy=0でσy=0,y=-bでσy=0,τxy=0と考えられるから,β=λbと置けば,

2.3.8 曲りばりの応力
図2.34には曲りばりの微小部分が示されている.弾性でHookeの法則とベルヌーイ(Bernoulli)の平面保持の法則が成り立つならば軸方向の応力σは,図のような軸力N(引張を正)と曲げモーメントMを受けたとき,
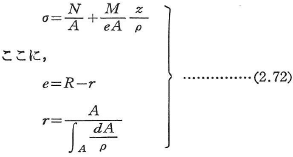
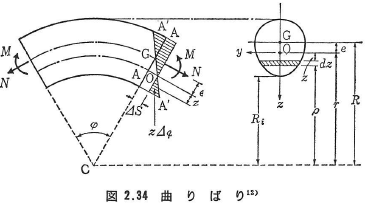
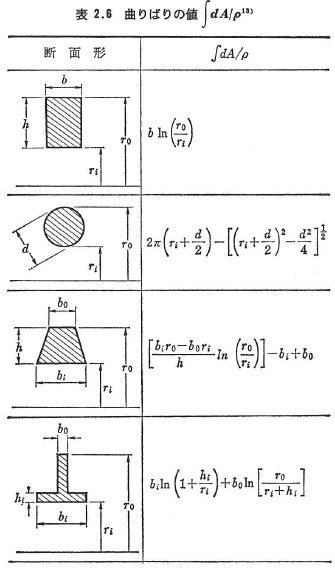
Rとeはそれぞれ曲率の中心Cより図心(重心)Gまでの距離,そして![]() なるような定点Oと図心G間の距離を示している.表2.6には曲りばりの典型的な断面の
なるような定点Oと図心G間の距離を示している.表2.6には曲りばりの典型的な断面の![]() ,すなわちA/rの値が与えられている.
,すなわちA/rの値が与えられている.
2.3.9 はりのたわみ
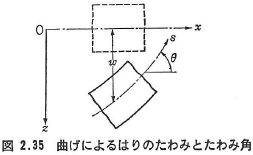
図2.35には,はりのたわみωとたわみ角θが示されているが,曲率をxとし,図のように下に凸のたわみが起こる場合を正と考える.はりの変形中の重心軸に沿った長さをsで表せば,
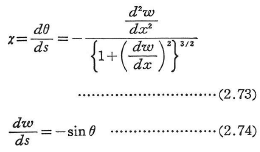
となるが,微小変形の場合,1≫(dω/dx)2であり,
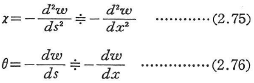
したがって,図2.23および式(2.49)から![]() =0のときは,
=0のときは,
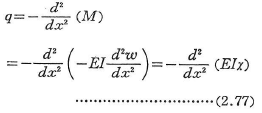
式(2.75)と式(2.77)を比較すれば,ωとMあるいはxとqとの相似関係が成立している.すなわち,ωは分布荷重xを受けるはりの曲げモーメントを意味しているし(弾性荷重),たわみ角はせん断力を意味していることがわかる.このようなはりのことを共役ばりといい,この関係をMohrの定理という.
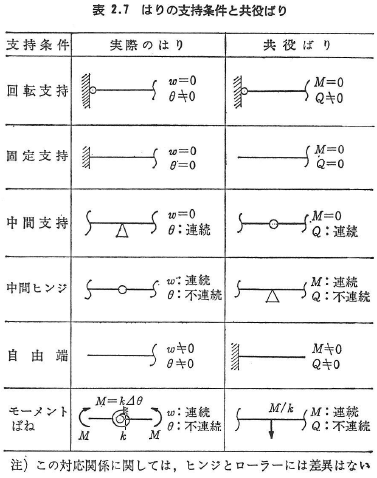
表2.7には,はりの典型的な支持状態と対応する共役ばりが示されている.この表において,ω,θは実際のはりのたわみ,たわみ角,また,M,Qはそれぞれ共役ばりの曲げモーメント,せん断力を表している.曲げの単位長さ当たりのひずみエネルギー密度をU,補ひずみエネルギー密度をU*とすれば,

一例として,材料が線形弾性のときは,

さらに,重心のせん断変形による弾性ひずみエネルギーUQはGをせん断弾性係数とすれば,

となる.ただし,kは次式より与えられる.

この式中のkは断面のせん断応力τを平均せん断応力で除した変数である.表2.5(a)にはせん断応力τの分布,ならびにkの断面内の最大値が代表的な断面についてそれぞれ与えられている.また代表的な断面のkの値も表2.5(b)に与えられている.
いま,ある仮想的な![]() を考え,その方向のたわみをδとすれば,式(2.79),(2.80)よりCastiglianoの定理を用いると,
を考え,その方向のたわみをδとすれば,式(2.79),(2.80)よりCastiglianoの定理を用いると,
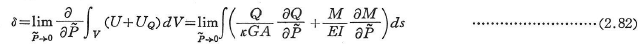
一方,曲線ばりに蓄えられる弾性ひずみエネルギーは,式(2.72)と(2.80)を考慮すれば以下のとおりとなる.
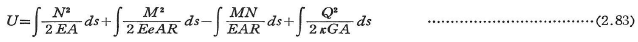
ここに,∫dsは曲線ばりの図心軸に沿った積分を意味する.したがって,荷重![]() を作用させ,その方向の作用点での変位δは変形が微小なとき,Castiglianoの定理より求められ,
を作用させ,その方向の作用点での変位δは変形が微小なとき,Castiglianoの定理より求められ,
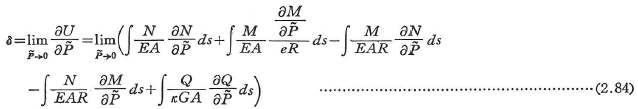
として与えられる.
2.3.10 軸力を受けるはりの塑性相関曲線
はりが純粋に曲げモーメントのみを受ける場合には,式(2.19)と式(2.20)より明らかなように,MY=WσYで縁応力が降伏応力に,MP=ZσYで全断面が塑性域に達する.
次に,曲げモーメントMのほかに軸力Nが作用する場合を考える.図2.36のように,高さdのはりを考え,中立軸とy軸の距離をηdとすれば,NY=AσYとして(e)図のような全塑性状態における軸力Nと曲げモーメントMの関係は,
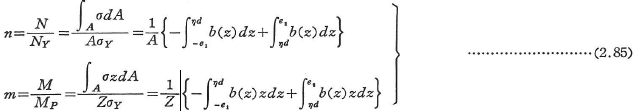
となる.ここに,z=-e1,e2は,それぞれはりの上面,下面を意味し,b(z)ははりの幅を表している.
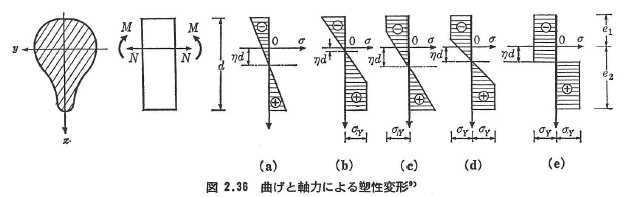
圧縮と引張が逆の場合には,式(2.85)で符号を逆転させればよい.このように考えれば,式(2.85)は助変数ηによって決まるmとnの相関曲線を表していること,また,この曲線で囲まれる内部の点では降伏応力よりも小さな応力が生じていることがわかる.この曲線は,はりの断面の降伏曲線といわれる.
例として,高さd,幅bの長方形断面のはりでは,

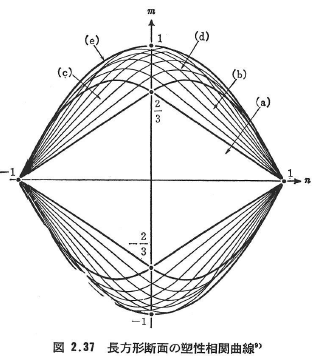
によって降伏曲線が与えられる.この曲線は図2.37中の曲線(e)として示されている.なお,図2.36に示されたその他の状態に対する降伏曲線も図2.37の中に図示されている.例えば一つの縁応力度が降伏応力に達するときの降伏曲線は4つの直線となり,

として表せる.さらに,一縁端降伏と両縁端降伏の境界を与えられる曲線は,正の曲げモーメントのみについて考えれば以下の2つの放物線で与えられる.
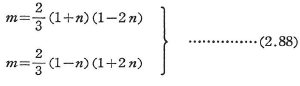
2.3.11 二軸曲げを受けるはりの完全塑性相関曲線
二軸対象断面の場合,軸力が零で二軸曲げを受けるときは中立軸は必ず図心を通る.
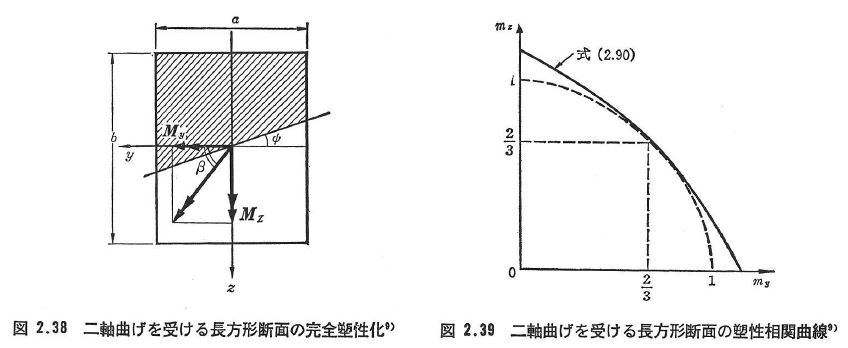
例として,図2.38のような長方形断面を考える.図2.24を参照して,My,Mzを中立軸とy軸のなす角ψを用いて表せば,いまψ≦tan-1(b/a)としたとき,

無次元化を行えば,

また,ψをMyとMzのなす角βにより表せば,

となる.さらに,境界線ψ=tan-1(b/a)のときMy=ab2σY/6,Mz=a2bσY/6であるから,mz=my=2/3であり,また,β=tan-1(a/b)=π/2-ψとなる.βとψの大きさがこれらの値より大きいときはy軸とz軸を入れ換えてやればよい.式(2.90)の相関曲線の1/4は図2.39により示される.
2.3.12 せん断と曲げの組み合わせを受けるはりの塑性相関曲線
次に,せん断曲げの組み合わせを考える.問題を簡単にするために,図2.23において,荷重はx-z面内に作用し,はりはこの面に関して対称断面を有するものとすれば,降伏条件は軸応力σとせん断応力τを用いて,

と書ける.α=2のときがTresca,α=√3のときがMisesの条件に対応する.曲げモーメントM,せん断力Qをσとτで表せば,

となるが,上界,下界の両定理の観点から,次の式がせん断と曲げの場合の降伏曲線を与えることがわかる.

ここに,νは1つの助変数である.
例として,上下左右対称のI型ばりで,厚さが断面寸法に比較して小さい場合には,全塑性モーメントMPと全塑性せん断力QPは,それぞれ,

ここに,
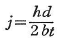
ただし,b,d,h,tはそれぞれフランジ幅,ウェブ高,ウェブ厚,フランジ厚を表す.無次元化された降伏曲線は次式で与えられる.
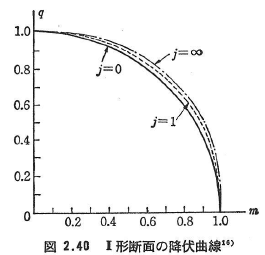
図2.40にはこの降伏曲線を与える.j=∞のときは長方形断面であり,j=0のときはウェブのない理想的なI形断面を示しm2+q2=1なる円である.
