Contents
2.1.1 図心と断面一次モーメント
図2.1に任意の形状の断面を示している.dAをこの断面内の微小面積としたとき,断面一次モーメントは次式で与えられる.
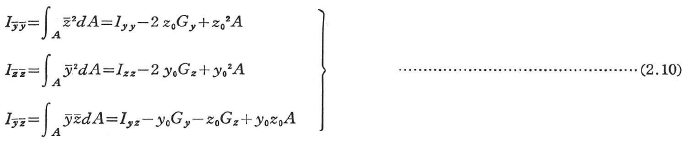
座標軸が平行移動した場合を図2.2に示すが,y,z軸まわりの一次モーメントをGy,Gzとしたとき,![]() 軸まわりの一次モーメント
軸まわりの一次モーメント![]() は次のように与えられる.
は次のように与えられる.
図心とは,1点を通る任意の直交軸まわりの断面一次モーメントがそれぞれ0であるような点である.図2.2において![]() 軸を図心を通るように選べば,y,z軸に関する図心位置(y0,z0)は次式で与えられる.
軸を図心を通るように選べば,y,z軸に関する図心位置(y0,z0)は次式で与えられる.

2.1.2 断面二次モーメント,断面相乗モーメント,断面二次半径,断面係数
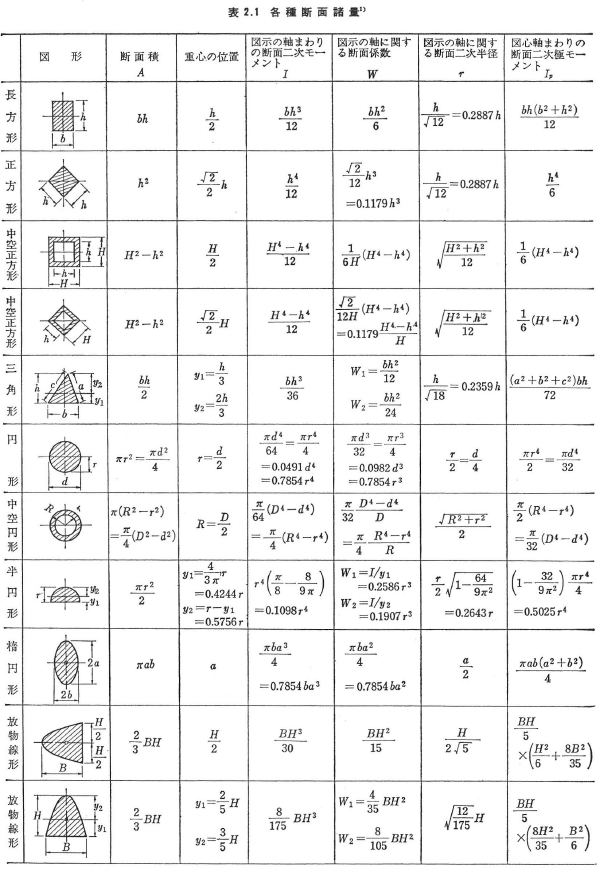
図2.1において次式で与えられる量を,それぞれy,z軸まわりの断面二次モーメントという.
また,断面相乗モーメントは次式により与えられる.

y,z軸方向の断面二次半径もしくは回転半径ry,rzは次式で与えられる.

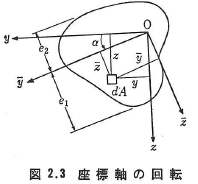
図2.3には,任意形状の断面と図心を通る軸およびこの一軸からの上下の最遠端までの距離e1,e2を示している.断面係数W1,W2は次のように定義される.

2.1.3 断面二次極モーメント,二次極半径
断面二次極モーメントIPは,図2.1において微小面積dAと断面に垂直な軸との間の距離をrとするとき,次式で与えられる.
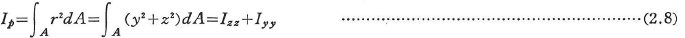
また,断面の二次極半径rpは次式で定義される.

各種の断面の諸量は表2.1に与えられている.
2.1.4 座標軸の移動と回転慣性楕円
図2.2に示されているように,直交直線座標軸y,zに平行な座標軸![]() まわりの断面二次モーメント
まわりの断面二次モーメント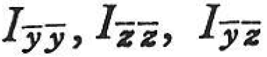 は次式で求められる.
は次式で求められる.
座標軸y,zが断面の図心を通るときは,

次に,図2.3のように,原点Oを共有し,直交直線座標軸y,zと反時計方向に角度αをなす直交直線座標軸![]() を考え,これらの軸まわりの二次の断面モーメント
を考え,これらの軸まわりの二次の断面モーメント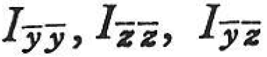 を求めると次式のようになる.
を求めると次式のようになる.

また,これらより,
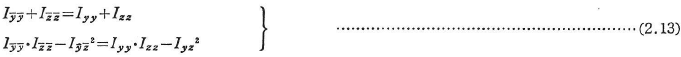
という関係が成り立つが,いずれも座標軸の取り方に関係のない値,すなわち不変量を示している.
図2.3において,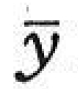 軸上に原点Oより線分
軸上に原点Oより線分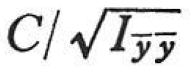 をとり,その端の点の座標をy,zとするとき(C:定数),
をとり,その端の点の座標をy,zとするとき(C:定数),

これを式(2.12)に代入すれば次式を得る.

これは大きさ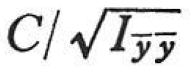 であるすべての線分の終端を結んで得られる曲線のy,zに関する方程式があり,断面の回転慣性楕円とよばれる.
であるすべての線分の終端を結んで得られる曲線のy,zに関する方程式があり,断面の回転慣性楕円とよばれる.
2.1.5 単純ねじりに関する断面定義
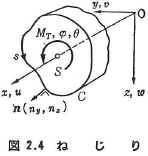
図2.4のように,一定断面の直線材にねじりモーメントMTが作用するとき,断面の回転角をφ,ねじり率をθとするとき,

ただし,Gはせん断弾性係数である.GJをSt.Venantのねじり剛性,あるいは,単にねじり剛性とよぶ.
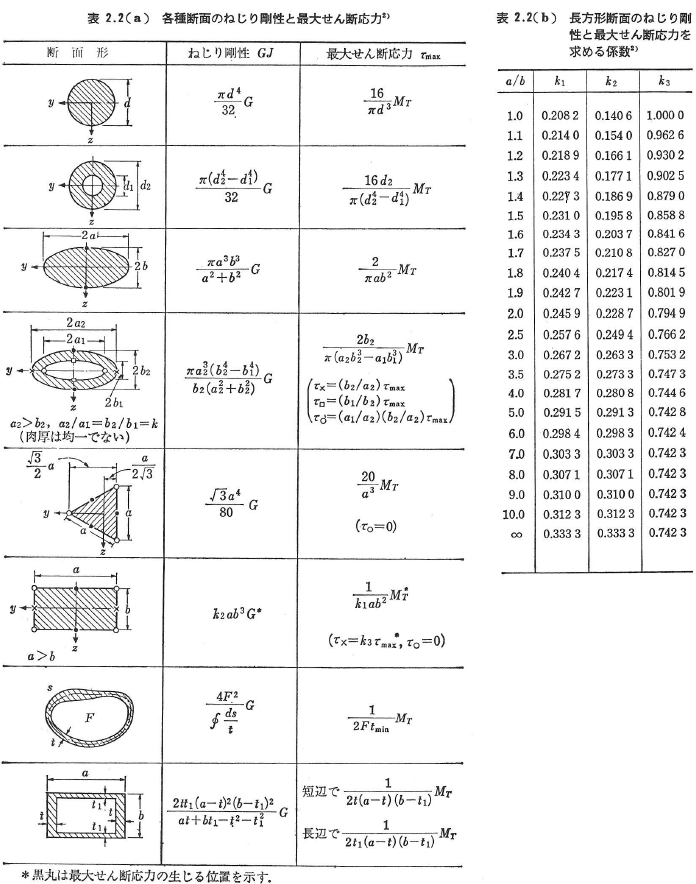
各種の断面のねじり剛性と最大せん断応力は表2.2(a)に与えられている.
2.1.6 せん断中心
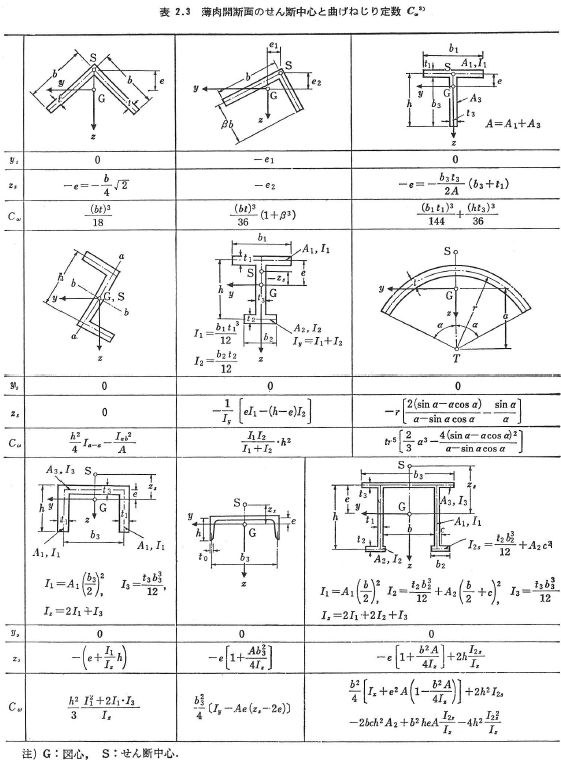
直線ばりにおいて,荷重の横断面方向の合力が断面内のある特定な点を通るときはねじりは生じない.このような点をせん断中心という.一対称軸を有する断面では,せん断中心はその対象軸上にあり,二対象軸を有する場面にはせん断中心と図心とは一致する.各種の薄肉開断面のせん断中心は表2.3に与えられている.
2.1.7 曲げねじり定数
円形断面以外の棒がねじりを受けると断面は一般に軸方向にそる.このそりがいろいろな原因により拘束されるときには軸方向応力を生じるし,単純ねじりモーメント以外に曲げねじりモーメント(そりねじりモーメントともいう)というねじりモーメントを生じる.
図2.5にはねじりを受ける任意薄肉部材の断面と側面が示されているが,MTは次式で表される.

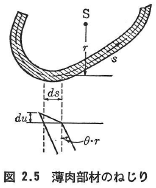
右辺第一項は単純ねじりモーメント,第二項が曲げねじりによるモーメントである.ECωは曲げねじり剛性とよばれる量であり,薄肉開断面の場合には次式で与えられる.

ただし,
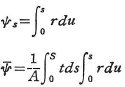
ここに,ωはそり関数とよばれ,A,t,S,そしてsあるいはuはそれぞれ,断面積,断面厚,断面の全長,そして断面に沿う長さを表し,rはせん断中心Sより断面の中心線上の任意点での接線にたてた垂線の長さを表している.
各種の薄肉開断面の曲げねじり剛性は表2.3に与えられている.なお,薄肉閉断面については2.4.7に述べられている.
2.1.8 塑性断面係数,形状係数
曲げの曲率をxとし,曲げによる緑応力が降伏応力σYに達したときの曲げモーメントおよび曲率をMY,xYとすれば,

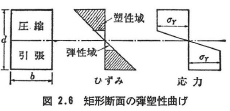
となる.さらにモーメントMをMYより増大させれば,はりは弾塑性になる.図2.6は例として,幅b,高さdの単純曲げを受ける矩形断面のはりを示すが,この極限状態においては断面の弾性部分は無限に小さくなり,断面の圧縮部は塑性圧縮,引張部は塑性引張を受ける.このときの曲げモーメントMPを全塑性モーメントと名付ける.
塑性断面係数Zは次式で定義される.
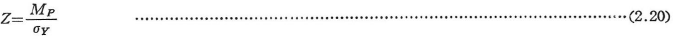
また,MPとMYの比,

を形状係数と名付ける.形状係数fの値は矩形断面については1.5であるが,その他の断面については1~2までの値をとる.
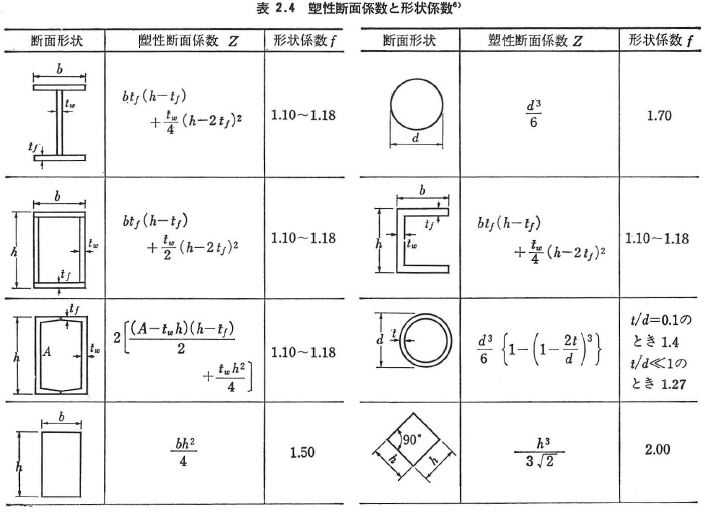
各種断面の塑性断面係数と形状係数は表2.4に与えられている.
2.1.9 塑性ねじり断面係数
棒がねじられると,最大せん断応力は表2.2からもわかるように,断面の周辺に生じる.さらに大きなねじりモーメントを受けると周辺部で塑性域に達し,極限状態では全断面が塑性域となる.このときのモーメントMTPを全塑性ねじりモーメントという.
塑性ねじり断面係数ZTは全塑性ねじりモーメントMTPと引張降伏応力σYとの比で定義される.

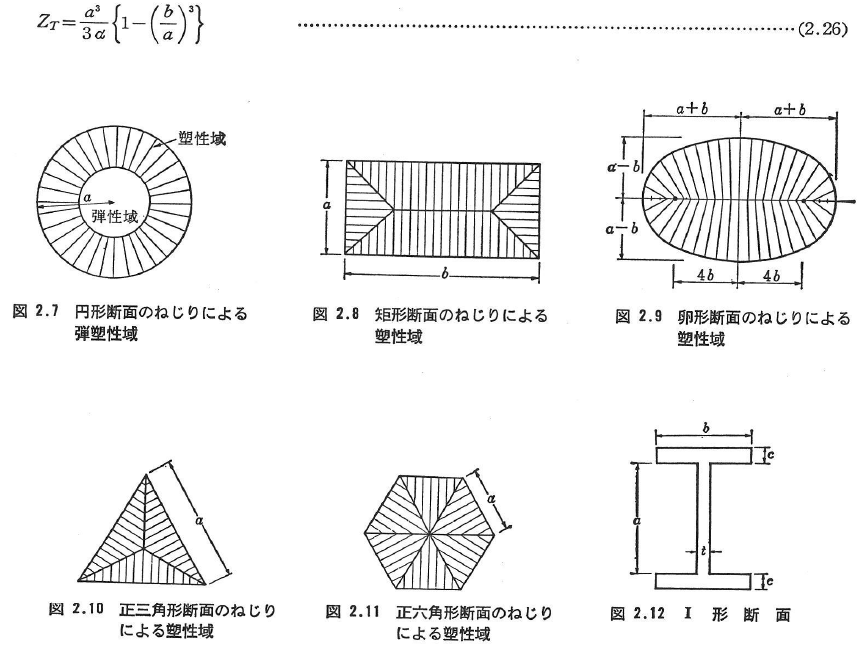
図2.7には半径aの円形断面の弾塑性ねじりが示されているが,この極限状態では全断面が塑性となり,塑性ねじり断面係数は,

ただし,αは定数であり,Mises,Trescaの降伏条件そ用いれば,αはそれぞれ√3と2である.
同様にして,外径2aで内径2bの中空円形断面のねじりに関しては,

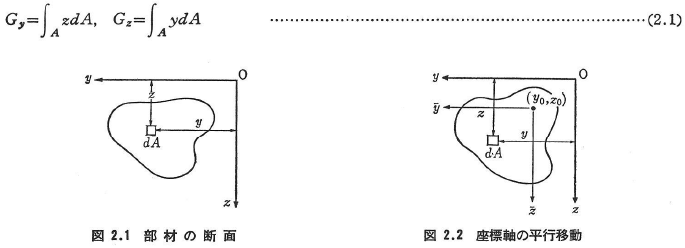
図2.8には,縦,横の長さがそれぞれa,bの矩形断面がねじりを受けて,極限状態に達している状態が示されているが,a≦bとしたとき,

また,辺の長さがa,bの中空正方形の場合には(a>b),