Contents
1.3.1 運動と変位
物体の運動は,物体中の粒子P(それを識別するために,ある基準時刻t0での座標 を用いる.これを物質座標という)が,時刻tで空間内に占める位置
を用いる.これを物質座標という)が,時刻tで空間内に占める位置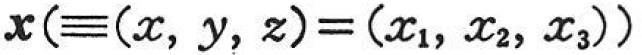 (空間座標という)を次の形で特定することにより表現される.
(空間座標という)を次の形で特定することにより表現される.
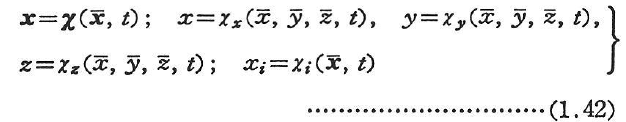
以下では,![]() ,すなわち
,すなわち![]() は
は![]() に関して微分できる関数とする.なお,簡単のために,関数表示
に関して微分できる関数とする.なお,簡単のために,関数表示![]() の代わりに直接
の代わりに直接![]() と書くこともある.また,
と書くこともある.また,![]() から逆に
から逆に![]() も定義される.
も定義される.
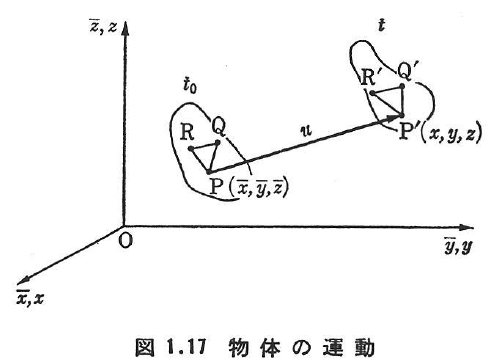
図1.17のように運動により,粒子P(その空間座標をPとする)がP’点に移動したとする.この際に生じるベクトル![]() を粒子Pの変位ベクトルという.変位ベクトルuの成分(u,v,ω);uiは次のように与えられる.
を粒子Pの変位ベクトルという.変位ベクトルuの成分(u,v,ω);uiは次のように与えられる.
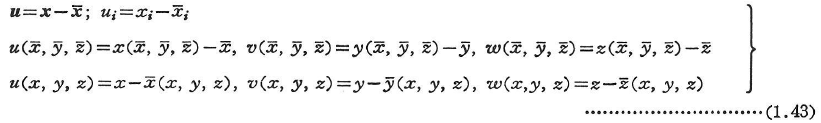
1.3.2 変形と変形勾配
図1.17に示すように,時刻t0での粒子Pと隣接した粒子Qの空間内の位置を![]() とする.これらの粒子が時刻tでそれぞれP’およびQ’に変位し,位置
とする.これらの粒子が時刻tでそれぞれP’およびQ’に変位し,位置![]() を占めたとする.すなわち,
を占めたとする.すなわち,
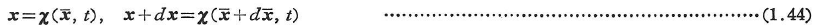
全微分dxの成分は,次のように表される.
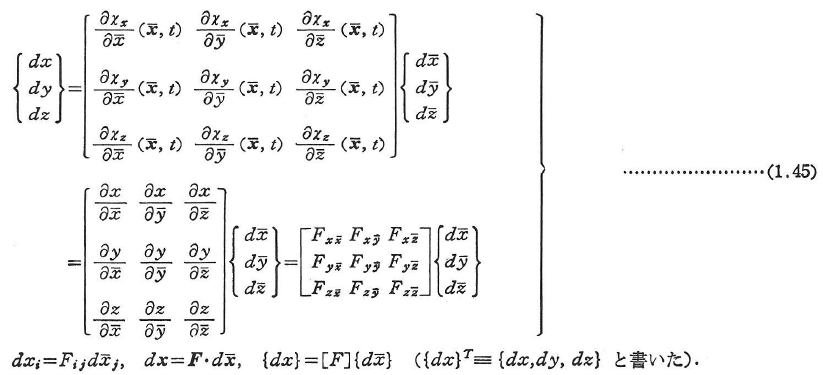
ここに,
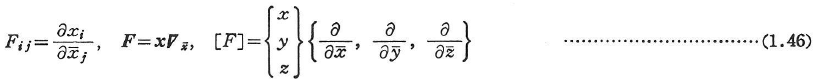
を変形勾配という.変形勾配は,変形と回転の程度を表す尺度である.
変形勾配Fは一意的に次のように分解される.これを極分解とよぶ.
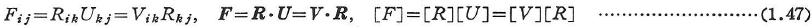
ここに,Rは回転,UおよびVは純変形(ストレッチ)を表している(F,R,U,Vは2階のテンソル,[F],[U],[V]はその行列表示)
1.3.3 ひずみ
物体の変形部分だけを表す尺度としてひずみを定義する.
(a)有限ひずみ
- コーシー-グリーン(Cauchy-Green)変形テンソルC,B;Cij,Bij
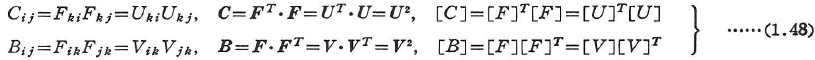
FT,[F]TはF,[F]の転置を表す. - 線素の変形前後の長さ(2乗)の差を取ると次のようになる.
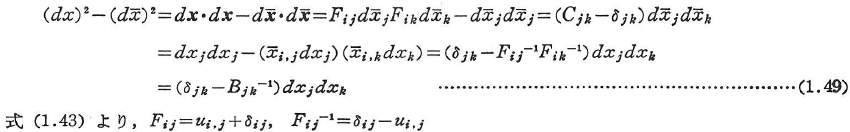
- ラグランジュ-グリーン(Lagrange-Green)のひずみテンソル
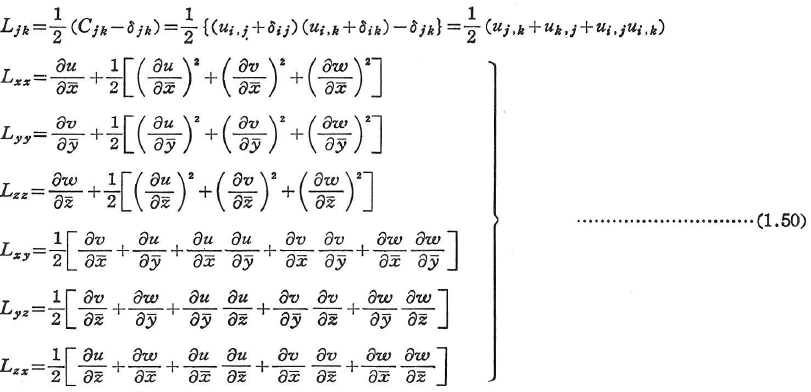
- オイラー-アルマンシ(Euler-Almansi)のひずみテンソル

ここに,Lxx,Lyy,…;L11,L22,…;Exx,Eyy,…;E11,E22,…は直ひずみとよばれ,Lxy,Lyz,…;L12,L23,…;Exy,Eyz,…;E12,E23,…はせん断ひずみとよばれる.上式からわかるように,ひずみテンソルは対象である.
(b)微小ひずみ
式(1.50),(1.51)において二次の項が一次の項に比して小さく省略できるとき微小ひずみという.なお,変位の勾配は,例えば
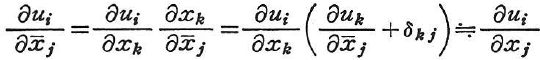
となって,物質座標と空間座標を区別する必要はなくなる.
微小ひずみは次のように変位と関係づけられる.

円柱座標系(r,θ,z)では次のようになる.
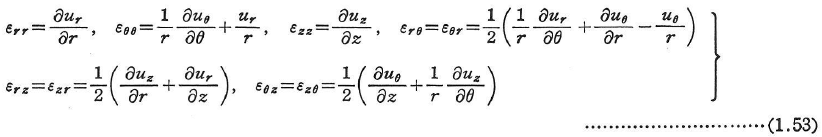
ここに,ur,uθ,uzはr,θ,z方向の変位を表す.
なお,ひずみテンソルの行列を次のように表す.

成分はεij;εxx,εxy,….
εxx,εyy,εzz;ε11,ε22,ε33を直ひずみ,εxy,εyz,εzx;ε12,ε23,ε31をせん断ひずみ,τij=2εij(i≠j)を工学的せん断ひずみという.
1.3.4 回転
(a)有限回転テンソル
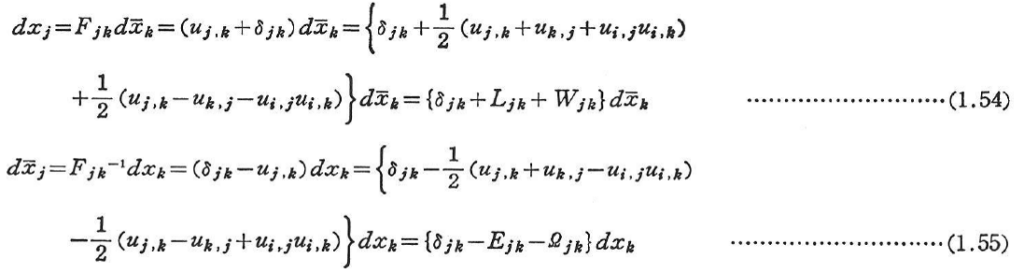
ここに,Wjk,QjkをLagrangeおよびEulerの回転テンソルという.
(b)微小回転テンソル
高次の項を省略すると,微小回転テンソルを得る.
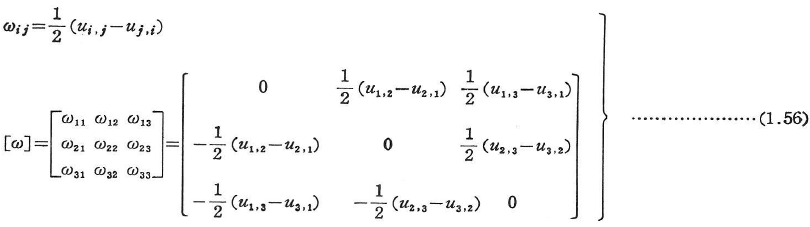
1.3.5 平面ひずみ状態
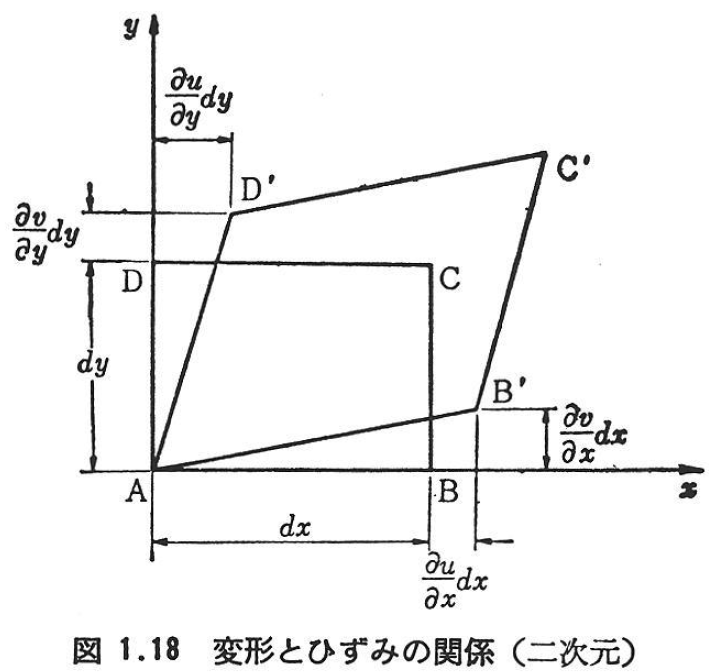
式(1.43)においてω=一定で,u=u(x,y),v=v(x,y)であればεzz=εxz=εyx=εzx=εzy=0となる.この状態は,平面変形,あるいは平面ひずみ状態とよばれる.
平面ひずみ状態での変形とひずみの関係を図1.18に示す.
工学的なせん断ひずみɤxy,ɤyz,ɤzxとしては,しばしば2εxy,2εyz,2εzxが用いられる.
1.3.6 主ひずみ,偏差ひずみ,八面体せん断ひずみ,相当ひずみ
(a)座標変換に伴う変位の変換
変位の変換則は座標変換の変換則と同じである.

lij(i=1,2,3)は,式(1.20)を参照のこと.u’,v’,ω’は座標系(x’,y’,z’)で表した時の変位である.
(b)ひずみの変換
ひずみの変換則は応力の変換則と同じである.
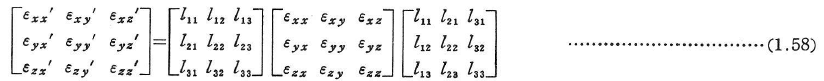
平面ひずみ状態では式(1.24)に対応して次式を得る.

(c)主ひずみ,偏差ひずみ,八面体ひずみ,相当ひずみ
主ひずみ,偏差ひずみに関しては,1.2.5で述べたことが,応力ひずみに読み替えるだけでそのまま成立する.主ひずみε1,ε2,ε3は次式を解いて求められる.
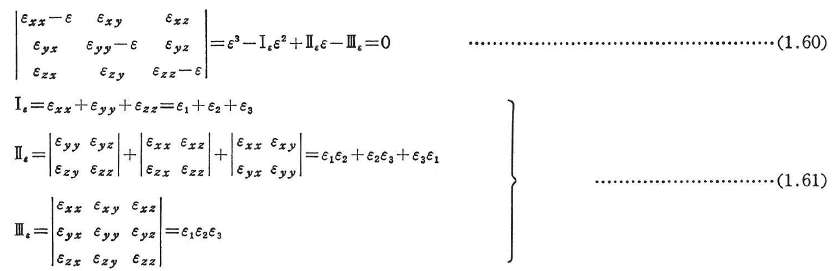
Ⅰε,Ⅱε,Ⅲεはひずみの第1,第2,第3不変量とよばれる.
平均直ひずみεmを,
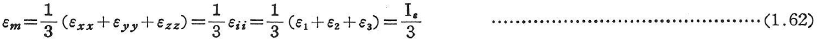
と書くと,偏差ひずみexx,exy,…;eijは次のようになる.
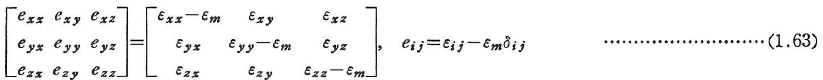
八面体直ひずみεoct,八面体せん断ひずみγoctは次のようになる.
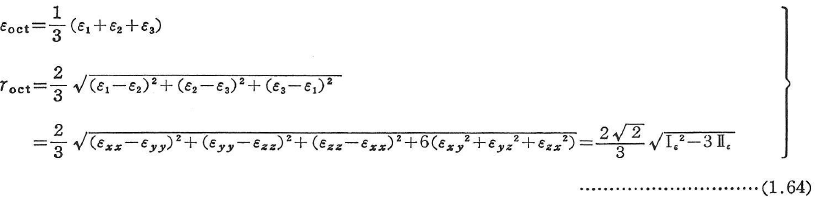
相当ひずみは,組合せ応力下のひずみを一軸応力状態の時に生じるひずみに換算したものである.例えば,せん断ひずみエネルギー説に従う相当応力σeqに対応して,相当塑性ひずみεeqpは(ε1p+ε2p+ε3p=0として)次のようになる(1.4.5参照).
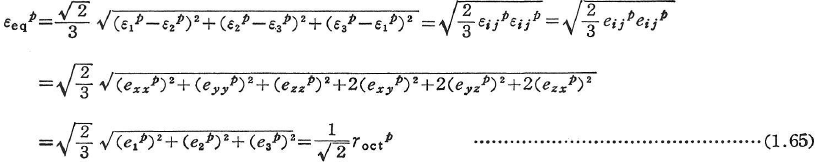
1.3.7 Mohrのひずみ円とひずみロゼット
(a)Mohrのひずみ円
応力の場合と同様にして求められる.平面ひずみ状態では,せん断ひずみとしては最初直行していた2方向間の角度が,変形後,直ひずみ方向から反時計方向にまわって増加した時を正とする.Mohrのひずみ円とひずみ状態の関係を図1.19に示す.
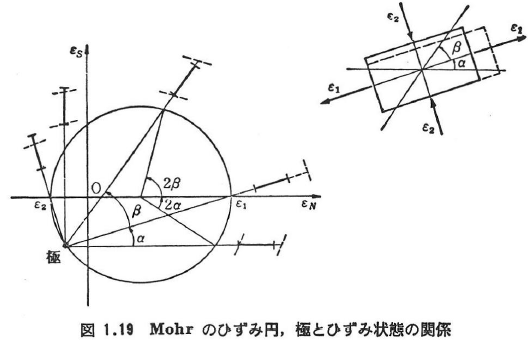
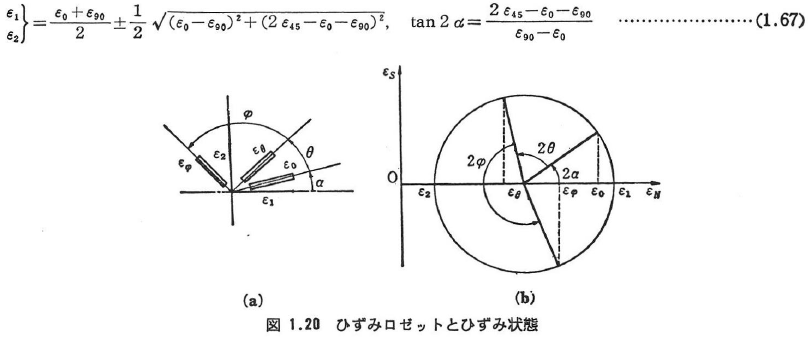
(b)ひずみロゼット
図1.20(a)に示すようなひずみロゼットを用いて,平面上の直ひずみε0,εθ,εφが求められるとすると,主ひずみおよび主ひずみの方向は次式より求められる.(図1.20(b)).
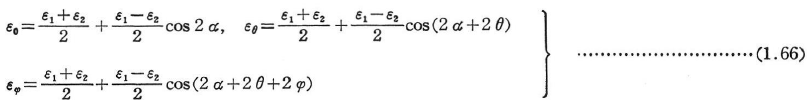
直角ロゼット(図1.20でθ=φ=45°)では次式を得る.
1.3.8 適合条件
式(1.52)でu,v,ω;uiを未知関数とする6つの式とみなすと,εxx,εyy,…;εijがある条件を満足するとき限り一意解が求められることになる.この条件は,適合(可積分)条件式とよばれる.適合条件式のうち次の6個だけが異なったものである.
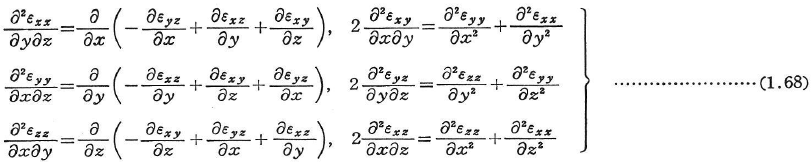
しかし,これらは完全に独立ではない.第1式をyで,第3式をxで微分して加えると,第2式をzで微分したものと等しくなる.同様の恒等式が合計3個得られる.このような式をビアンキ(Bianchi)の恒等式という.有限ひずみに対しても同様に,条件式が得られるが,複雑となるので省略する.
