1.5.1 弾性問題の基礎方程式
微小変形弾性問題の基礎方程式は,つり合い方程式(1.17)3個,ひずみと変位の関係式(1.52)6個,応力とひずみの関係式(1.91)6個,計15個の方程式である.これに対して,未知量は応力6個,ひずみ6個,変位3個,計15個である.したがって,弾性学の問題は与えられた境界条件のもとで,これら15個の基礎方程式を解くことに帰着される.解法は変位法と応力法に分けられる.以下等方性の場合について述べる.
(a)変位法
変位法では,変位成分が未知関数である.応力とひずみの関係式(1.94)およびひずみと変位の関係式(1.52)を用いて応力を変位成分で表し,これをつり合い方程式(1.17)に代入すると,変位に関する基礎方程式(ナヴィエ(Navier)の式)を得る.
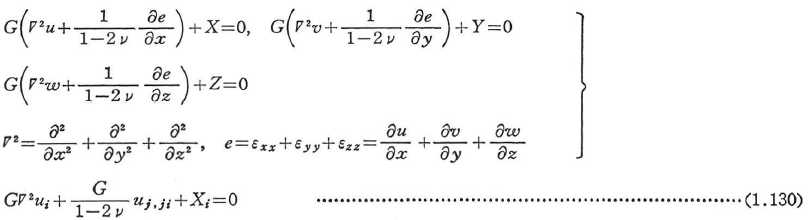
弾性問題は与えられた境界条件のもとで上式を解くと帰着される.
(b)応力法
応力法では応力成分が未知関数である.応力法ではひずみと変位の関係式と等価な適合条件式(1.68)を用い,そのひずみ成分を応力とひずみの関係式(1.94)を用いて応力成分で表した適合条件式(ベルトラミ-ミッチェル(Beltrami-Michell)式)は,次のようになる.

(c)エアリー(Airy)の応力関数
二次元弾性問題を応力法で解く際には,次のような関数Φ,
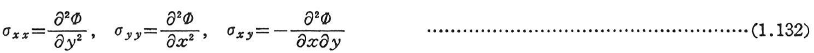
を導入すると,つり合い方程式(1.17)は常に満足される(ここでは,簡単のために物体力はないものとした).したがって,問題となるのはBeltrami-Michellの式だけとなる.二次元問題のBeltrami-Michellの式に,式(1.132)の応力を代入すると次の重調和方程式を得る.

この重調和関数Φは,Airyの応力関数とよばれる.二次元弾性問題は式(1.133)を与えられた境界条件のもとで解くことに帰着される.
なお,平面応力問題におけるポアソン比νの代わりにν/(1-ν)を代入すると対応する平面ひずみ問題が得られ,また,平面ひずみ問題のνの代わりにν/(1+ν)を代入すると対応する平面応力問題が得られる.
1.5.2 粘弾性問題の基礎方程式
等方線形粘弾性体の基礎方程式は,構成式(1.101)または(1.102)を除けば弾性の場合とまったく同じである.ただし,応力,ひずみ,変位はすべて時間の関数となっていることに注意されたい.
初期値-境界値問題の解法は1.5.1に準じればよい.なお,問題によれば,弾性-粘弾性対応原理(1.4.4(c)参照)が適用できる.
1.5.3 弾塑性問題の基礎式
弾塑性問題の基礎式は増分形で表される.ここでは,簡単のために増分を で示す.
で示す.

弾性問題と異なる点は,増分形になっていることと構成式だけである.解法は1.5.1に準じればよい.
1.5.4 有限要素法
境界値問題の正解を求めることは一般に困難であり,幾多の近似解法が試みられてきた.数値解法としては有限要素法が最も汎用性が高く,広く用いられる.
有限要素法は,連続体をモデル化して仮想的に有限個の要素(部分)が有限個の点ないし,線,面で結合した集合体であると見なし,このようなモデル(有限要素モデル)について,個々の要素の特性を求め,あるいは簡単な特性を仮定したうえで,要素間の結合条件ならびに境界条件を満たす解を見出すことにより,そのモデル全体にわたる挙動を解析する方法であるといえる.弾性問題を例に変位法による手続を示す.
- 対象物体を仮想の境界線,面によって有限個の”要素”に分割する(有限要素モデルの構成).
- 個々の要素の変位を適当な近似関数を用いて表す(変位関数の仮定).

{u}は変位成分ukの列ベクトル,{δ}は節点での変位成分δmより成る列ベクトル,[N]は変位を与える形状関数(基底関数)より成る行列,行列要素はNkm. - ひずみを節点変位の関数として表現する({ε}は列ベクトル表現,式(1.91)参照).

応力を求める(初期ひずみを{ε0}とする).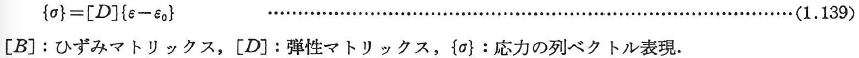
- 要素の節点での力と変位の関係を求める.例えば,仮想仕事の原理(式(1.204)参照)より次式をえる.
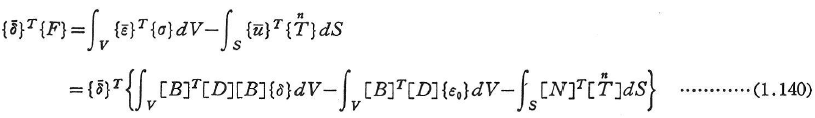
仮想変位は任意に取り得るので次式を得る.
等価節点力を左辺へ移したものを改めて{F}と書くと,要素特性は次のように書ける.
- 各節点の力のつり合い条件から系全体の特性を表す方程式を構成する(系全体の特性の表現).すべての節点に対して,節点変位と節点での合力{R}との関係,

[K]の行列要素Kijは節点jを共有するすべての要素のその節点に対応した行列要素の和で与えられる.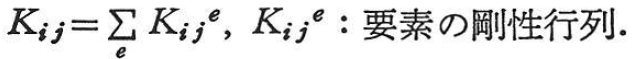
- 未知節点変位{δα},既知節点変位{δβ}を用いて,式(1.143)を次のように分ける.

ここに,{Rα}は外荷重,{Rβ}は反力である.
未知変位を求める.
反力は次式より求まる.
- 応力を求まる(式(1.139))

