Contents
1.1.1 力とモーメント
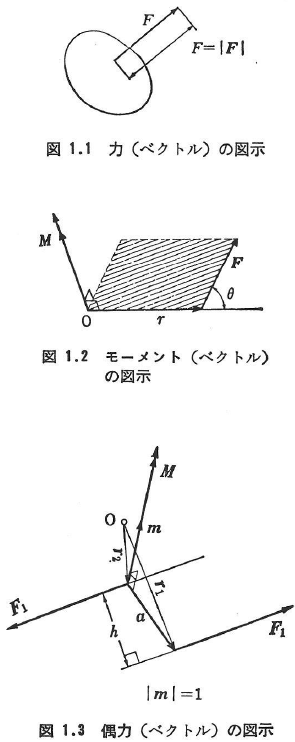
(a)力
- 力の3要素 大きさ,方向,および作用位置
- 力の表示 ①図示的表示(図1.1):力の大きさは線分の長さで,方向は矢印の向きで,作用点は線分の始終点で表す.②数学的表示:ベクトル量Fで表す.
(b)力のモーメント
1点Oまわりの力のモーメントMは,
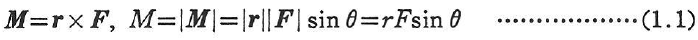
ここに,r,Fは図1.2に示すようなベクトル量であり,r,Fはその大きさとする.
モーメントの大きさは,rとFを相隣る両辺とする平行四辺形の面積に等しく,その方向は,この平行四辺形を含む面に垂直で,右手系法則に従う.モーメント(ベクトル)は,二重矢印を付けた線分(図1.2)あるいは矢印を付けた円弧で表す.
(c)偶力
- 定義 互いに平行で反対向きに作用する2個の同じ大きさの力(ベクトル)の組を偶力とよぶ(図1.3).
- 偶力によるモーメントM
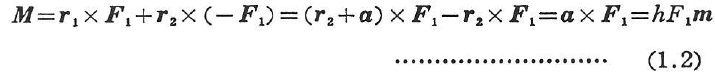
ここに用いた記号は図1.3を参照されたい.
1.1.2 力の合成と分解
(a)1点に働く力の合成と分解
- 定義 同一の作用点に働く多数の力(ベクトル)は,系に何ら影響を与えることなく,それらのベクトル和に等しい単一の力(ベクトル)に置き換えることができる.この操作を力の合成とよび,置き換えて得られた力を合力とよぶ.力の合成の逆の操作を力の分解とよぶ.
- 力の合成と分解の公式
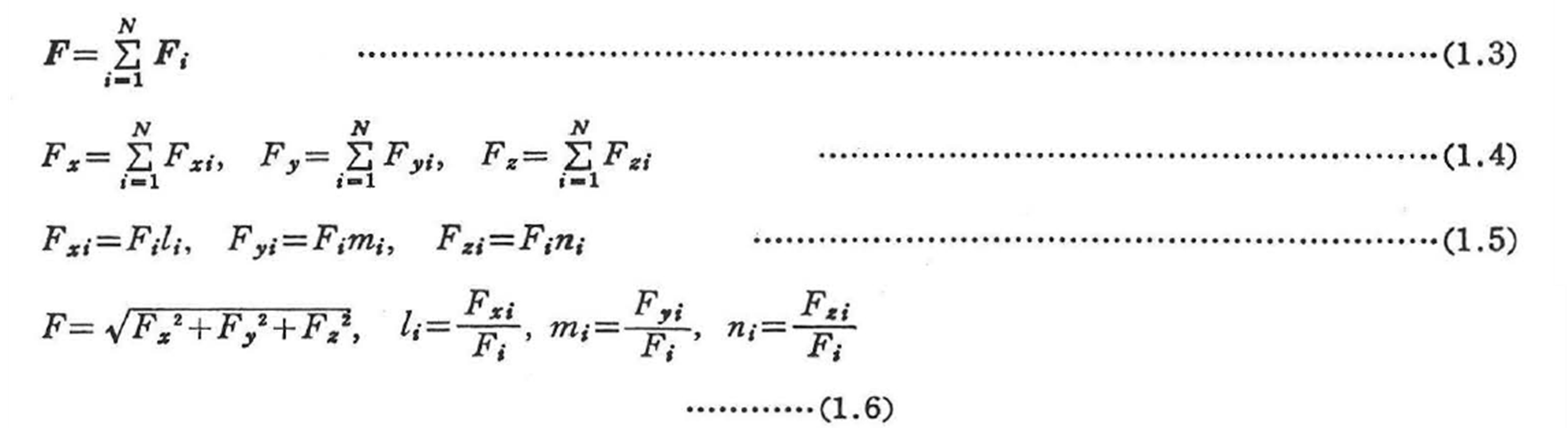
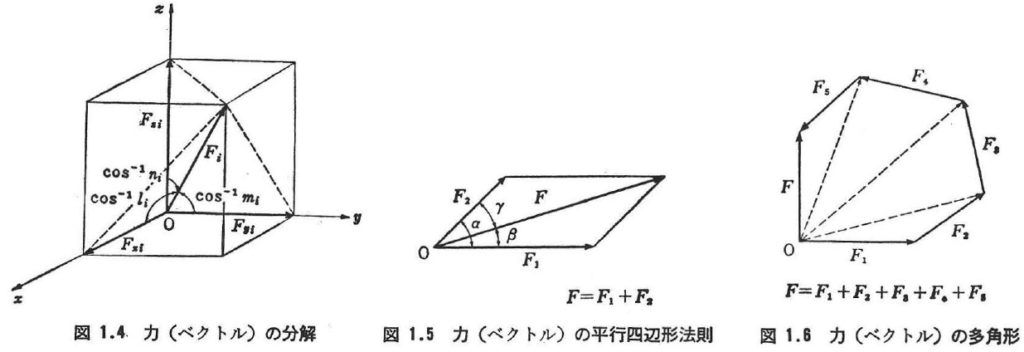
ここに,F1,F2,…FN,は1点に働く力(ベクトル)を,Fはその合力(ベクトル)を,Fx,Fy,FzはFは直交直線座標(x,y,z)でのx-,y-,z-軸方向成分をFxi,Fyi,Fziは,Fiのx-,y-,z-軸方向成分を,li,mi,niはFi方向の方向余弦を表す(図1.4) - 平行四辺形法則と力の多角形(図1.5,1.6)
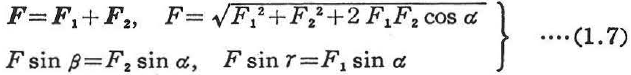
ここに,Fは両側辺をF1,F2とする平行四辺形の対角線の一つを表している.
1点に作用する2個以上の力の合成は,2力ずつの合成の操作を順次,繰り返して行えばよい.特に,一平面上の1点に作用する力の合成は,図示的には多角形となる.これを力の多角形とよぶ.
(b)偶力によるモーメントの合成
偶力によるモーメントはベクトル量であり,力(ベクトル)の場合と同様な合成ならびに分解法則が成り立つ.
(c)力の力と偶力への分解
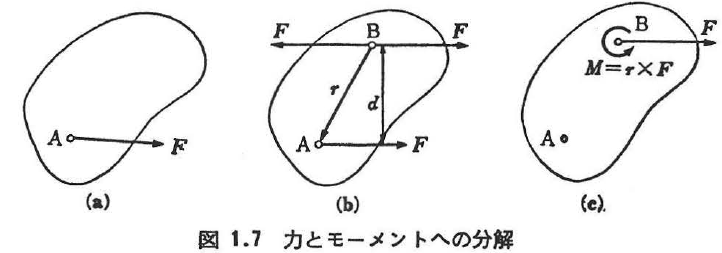
図1.7(a)に示すように,剛体のA点に力Fが作用しているものとすると,これは,重ね合わせの法則によって図1.7(b)に示すような3力が作用する場合と同じであり,さらに偶力を用いると,図1.7(c)に示すようになる.すなわち,A点に作用する力Fは,B点に作用する同じ力Fと,前者のB点まわりのモーメントM=r×F(rはB点からA点に向かうベクトル)で置き換えられる.
(d)1点に作用しない力の合成
ある物体に作用するすべての力(ベクトル)について1.1.2(c)の操作を行えば,ある1点Oに作用する合力(ベクトル)と合モーメント(ベクトル)が求まる.

ここに,Fは合力(ベクトル),Mは合モーメント(ベクトル),Fxi,Fyi,Fzi,Mxi,Myi,Mziは力(ベクトル)Fi,モーメント(ベクトル)Miの直交直線座標方向成分である.
1.1.3 力のつり合い
- 定義 力の作用のもとで,物体が移動および回転を起こさない状態にあるとき,その物体はつり合い状態にあるという.また,そのときの力はつり合っているという.
- 変形し得る物体がつり合い状態にあるための必要十分条件は,「その系に作用するすべての外力およびその系から切り離して考え得るすべての部分系に作用するすべての外力の合力が0であり,かつ,任意の点に関するすべての外力の合モーメントが0である」ことである.

1.1.4 外力と内力,断面力
- 定義 外力とは,対象とする物体系の外より作用する力であり,①表面に作用する表面力と,②質点に作用する物体力に分けられる.内力とは物体が一定の形を保持するために物体系内の仮想の断面相互間に働く力であり,応力ともよばれる.対象とする系のある断面上に働く内力(応力)のその断面にわたる合力は,断面力(部材力)とよばれる(応力について1.2.1を参照のこと).
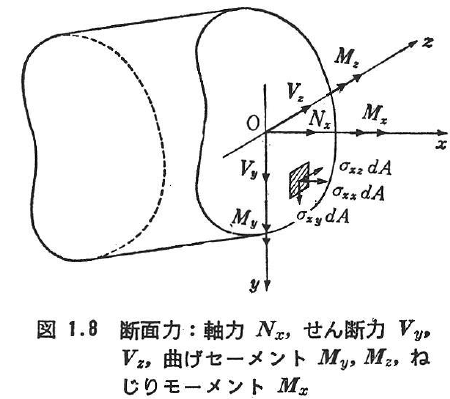
- 断面力
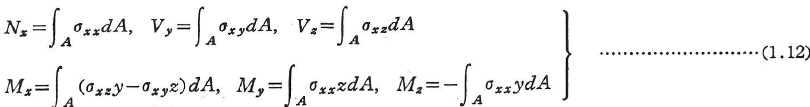
ここに使用した記号は,図1.8を参照されたい.
Nxは軸力,Vy,Vzはせん断力,My,Mzは曲げモーメント,Mxはねじりモーメントとよばれる.