図6.11に示す不静定トラスを解く（節点４の変位と各部材力を求める）場合を例に説明する．すべての部材について断面積はA，ヤング率はEとする．部材座標は節点番号の小さい方から大きい方に向かって設定するものとし，全体座標系のX軸から時計回りに各部材座標系のx軸までの角をそれぞれθ14，θ24，θ34とする．

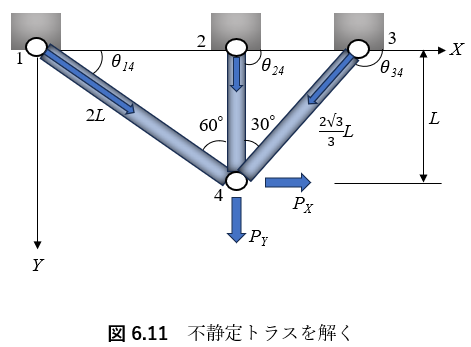
　部材座標1-4の部材座標に関する剛性方程式は，次式のようになる．

座標変換行列は，cosθ14=√3/2，sinθ14=1/2であるから，式(6.49)を用いて

となる．全体座標系での剛性マトリクスK14は，K14=T^T14・k14・T14を計算するか，式(6.60)の結果を用いて，次式のように得られる．

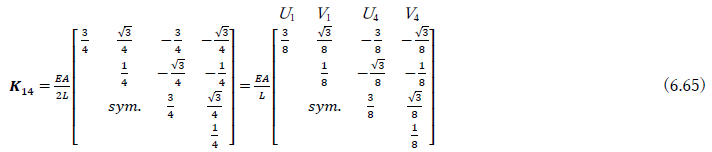
同様に，部材2-4の部材座標に関する剛性方程式と座標変換行列は，cosθ₂₄=0，sinθ₂₄=1であるから

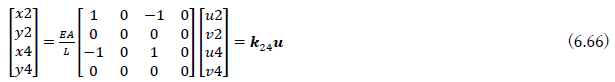
となり，全体座標系での剛性マトリクスK24は，次のようになる．

　次に，部材3-4の部材座標に関する剛性方程式と座標変換行列はcosθ₃₄=-1/2，sinθ₃₄=√3/2であるから

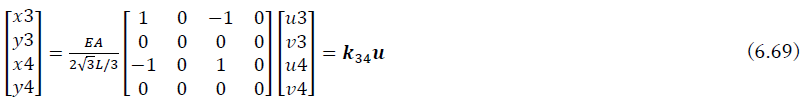
となる．したがって，全体座標系での剛性マトリクスK34は

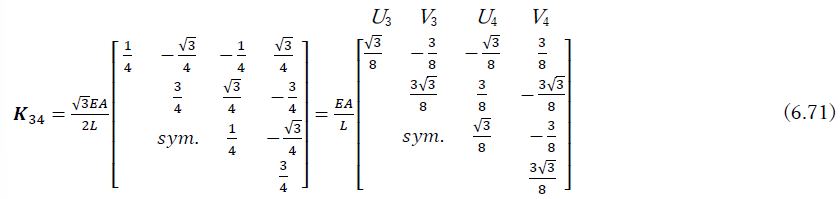
となる．構造全体の剛性方程式の枠をつくって，式(6.65),(6.68),(6.71)を該当する位置に足し込むと，下記の式を得る．

荷重条件X₄=P_X，Y₄=P_Yと境界条件U₁=V₁=U₂=V₂=U₃=V₃=0を考慮すると

となる．未知変位について解くと

となる．未知反力は

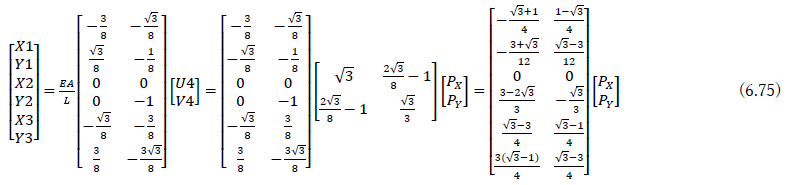
として求められる．　
　部材力N₁₄，N₂₄，N₃₄は，式(6.74)を式(6.62)に用いて，それぞれ次のようになる．

　　

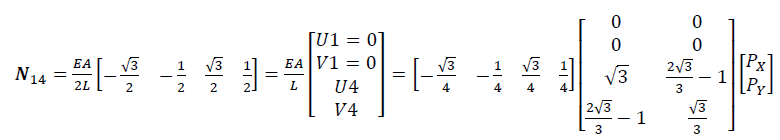
ここで，例えば，P_X=0，P_Y=Pとおくと，式(6.76)~(6.78)より，N₁₄=(3-√3)P/6，N₂₄=√3P/3，N₃₄=(√3-1)P/2，また式(6.74)よりV₄=√3LP/(3EA)となる．

ここで，演習問題6.4を解いてみよう．⇒malme.app/news/演習問題/