2.4.1　基本事項

　円形断面の棒がねじりを受けると，ねじりは棒の全長にわたって平等に生じ，断面内の点は円の中心点まわりに回転し，軸方向の変位，すなわちそりは存在しない．このようなねじりを単純ねじり，もしくはサン・ブナン（St. Venant）のねじりという．しかしながら，円形以外の断面がねじりを受けると一般にそりが存在する．このそりが何らかの形で拘束されれば局部的に軸力が生じ，また，単純ねじりモーメントのほかにそりの拘束に伴うねじりモーメントが生じる．このようなねじりを曲げねじり（そりねじり）とよんでいる．

　一定断面の直線材にねじりモーメントM_Tが作用するとき，軸方向のねじり率θとM_Tの関係は式（2.16）で与えられる．

　図2.4にあるように，断面内にy，z軸をとり，原点をせん断中心に一致させるならば，x=0で回転がない場合，ねじり率をθ，回転角をφとし，変位を（u，v，w）で表せば，

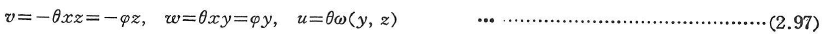
と書ける．ここに，ω（y，z）はSt. Venantのそり関数であり，

ここに，n（n_y，n_z）は境界線C上にたてた，法線方向の単位ベクトルである．

　ωの代わりに，その共役調和関数Ωを用いれば基礎方程式は，

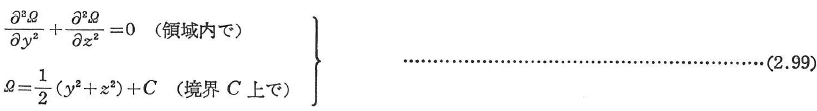
　一方プラントル（Prandtl）が考えた応力関数Φを使えば，

であり，基礎式は次のようになる．

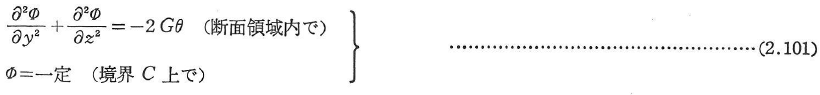
2.4.2　円形断面部材の単純ねじり

円形断面では，表2.2(a)にあるように

中空円形断面ではd₁内径，d₂を外径とすれば，同表より

2.4.3　任意断面部材の単純ねじり

2.4.1において述べられているように，そり関数ω，あるいはΩ，もしくは応力関数Φを求めればよい．

そり関数ωを用いれば，ねじり定数Jは次のようになる．

　一方，応力関数Φを用いれば，ねじりモーメントM_Tは，

例えば，境界線が(y/a)²+(z/b)²=1で与えられるような楕円形断面では，

と置き，式（2.16），（2.101），（2.106）を用いれば以下のようになる．

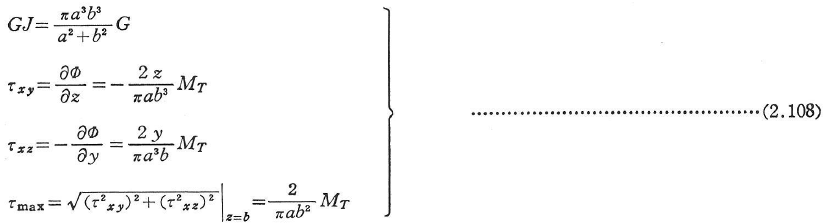
　特別な例として，a=b=d/2とおけば前述の2.4.2の円形断面のねじり問題が解けることになる．

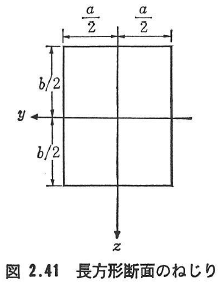
　また，図2.41のような長方形断面ではレヴィ（Levy）の級数を用いて（表2.2参照），

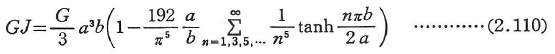
2.4.4　薄膜相似

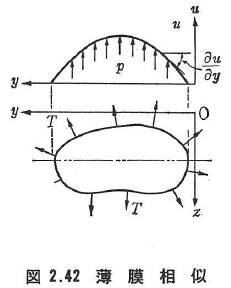
　棒の断面と同じ形状の穴をつくり，この上に石鹸膜をはり，図2.42のように圧力pをかける．この膜の境界に沿って働く一様な水平張力を単位長さ当たりT，たわみをuとすれば，

2.4.5　薄肉断面部材の単純ねじり

　薄肉断面では，①板厚方向の応力は小さく無視できる．②板の面内応力は板厚にわたって一定と考える．

　図2.43には薄肉一室断面部材が示されている．薄板の中心線に沿った長さをs，板厚をt，斜線を施した部分の面積をFとすれば，s方向のせん断応力τ_sは，

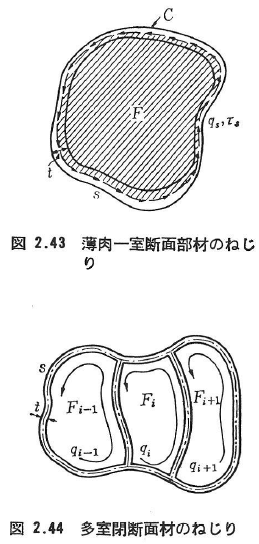
　図2.44には多室（n室）閉断面材が示されているが，この場合，第i室まわりのせん断流をq_iとすれば，第i室と第i+1室の境界壁でのせん断流q_sは力のつり合いから，

いま，

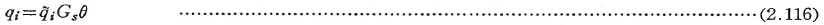
と置けば，式（2.62）のn_gを用いて，

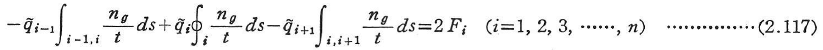
　ただし，F_iは薄板の中心線で囲まれる第i室の面積，∫_i-1,iは第i-1室と第i室の境界壁に沿う積分を表す．

　薄肉開断面では，閉断面と異なり，せん断応力は断面の縁に沿って一巡するように働くが，これは石鹸膜相似よりも容易に推測できる．開断面のねじり剛性ならびに最大せん断応力は，それぞれ，

ここに，G_j，b_j，t_jは，それぞれ第j部分のせん断弾性係数，断面の長さ，厚さである．

2.4.6　薄肉断面部材の非対称曲げ

　はりに横荷重が作用する場合，非対称曲げの場合でも荷重が断面のせん断中心を通るときは，ねじりは生じない．せん断中心は表2.3でも明らかなように，特に薄肉開断面においては，重心とかなり離れる場合が少なくない．横荷重がせん断中心を通る場合は曲げのみが作用すると考えられるが，薄肉開断面材でもベルヌーイ（Bernoulli）の平面保持の法則が成立するのが実験により一般的に認められている．薄肉閉断面材に曲げが作用した場合でも，平面保持が成立すると考えられる．しかしながら，室の幅が高さより極端に大きな場合や，断面形状にゆがみが生じる場合にはこの平面保持は崩れる．

2.4.7　そり拘束を受ける薄肉断面部材のねじり

　曲げねじりは2.1.7に述べられている．式（2.97）にあるように，そり関数ω_sを用いれば，軸方向すなわちx方向のそりuは，

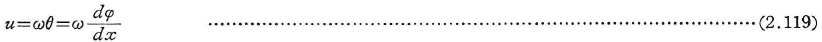
　薄肉開断面では式（2.18）より，薄肉閉断面では，

ここに，ω₀は，

より決定される．

　そりが拘束されると，軸応力σ_xが生じるが，

　また，そりの拘束に伴う二次的なねじりモーメントM_ωは式（2.17）の右辺第2項で与えられる．

2.4.8　ねじり部材の降伏条件

　部材が単純ねじりを受けるとき，せん断応力τ_xy，τ_xzが生じるが，合応力τは，

よって，塑性条件式は，

と書ける．ただし，αは定数であり，式（2.23）で説明されている．

　いま，Prandtlの応力関数Φを用いれば，式（2.101）より塑性条件式（2.124）は次のように書ける．

　したがって，石鹸膜相似により，塑性域では膜の最大傾斜角｜grad u｜は一定である．このことより，塑性状態では断面の形の板の上に砂をふりかけてできる砂丘によって類似されることがわかる．この類似を砂丘の類似とよぶのは上の理由による．

　各種断面の塑性ねじりについては2.1.9に述べられている．

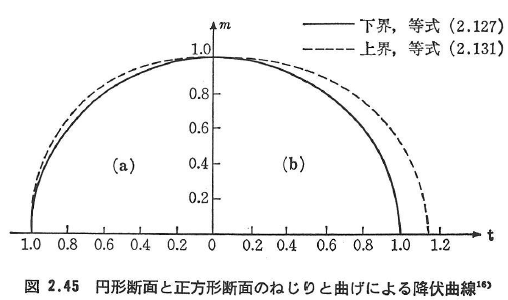
　曲げとねじりが同時に作用する場合の曲げモーメントMとねじりモーメントM_Tに関する塑性条件式は，一般的には厳密解としては得られない．したがって，降伏曲線の上界と下界を求めるのが合理的である．

　いま，ねじりによるせん断力τのみについては，単純ねじりを受ける場合の塑性域での応力分布，また，曲げ応力σについては，単純曲げを受ける場合の塑性域での応力分布を考えれば，それぞれにおいて力のつり合いを満足するし，絶対値を，

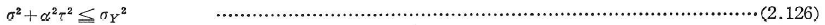
によって定めれば，応力は静的に許容であり，上の関係を用いればM，M_Tの相関関係は，

これは下界を与えるものである．ここに，M_P，M_TPはそれぞれ全塑性曲げモーメントと全塑性ねじりモーメントを表す．

　図2.4のように座標系をとったとき，純曲げの場合のy軸まわりの曲げ曲率を式（2.51）のようにとり，，また純ねじりの場合のねじり率を式（2.97）のようにとり，θで表せば対称断面の場合はひずみ速度はねじりに伴うそりの速度を無視すれば，

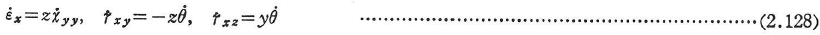
　これは運動学的に許容されるひずみ速度を表している．

　いま，塑性ひずみ速度の比例定数をλとすれば式（2.126）より，

　また，式（2.126），（2.128），（2.129）より比例定数λは，

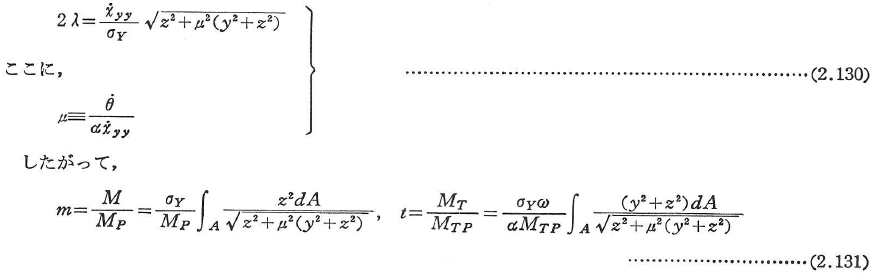
　式（2.131）はωを助変数とするmとtの関係を示し，上界を与えるものである．

　図2.45は（a）円形断面の，（b）正方形断面の相関曲線を示す．

　その他，折線で近似することもできるが，文献によられたい．