剛性マトリクスによりトラスを解く

 

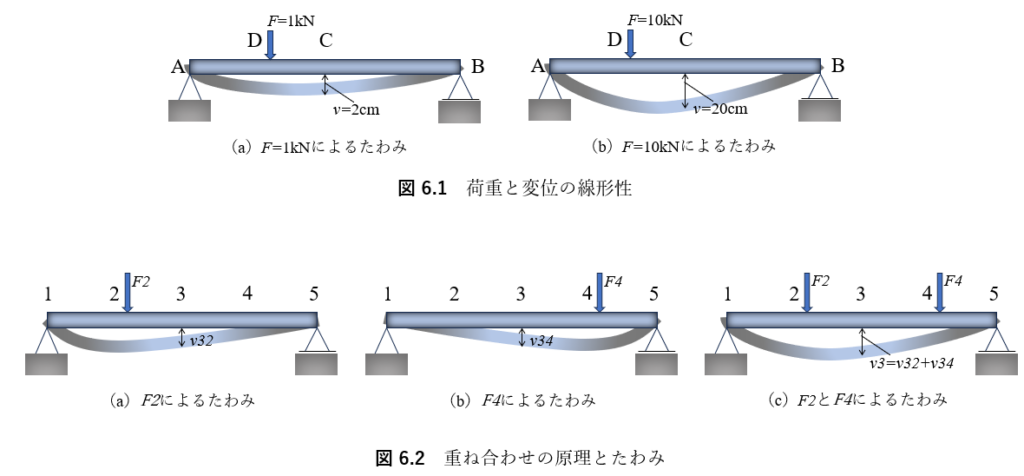
剛性マトリクス・・・ 支間lの単純ばりの中央に荷重 F が作用する場合の支間中央のたわみが ν={∫³/(48EI)}・Fで表されることなどからわかるように，弾性構造物のたわみは荷重と比例し，線形関係にある．すなわち，図6.1(a)に示すように，F=1kN が作用するときの着目点Cのたわみがν=2cmなら，F=10kNのときの同じ点のたわみは20cmになる．（図(b)参照）．さらに，図6.2(c)に示すように，F₂とF₄が同時に作用するときのたわみν₃は，F₂のみが作用したときのたわみν₃₂（図(b)参照）の和として求められる．これを重ね合せの原理という．

この二つの性質を使うと，各点のたわみと各点に作用する荷重との一般的な関係を導くことができる．まず，図6.3(a)に示すように，剛体運動をしないとうに拘束されている弾性構造物を考え，節点1～nを任意に定める．節点1、2、・・・、i、・・・、nに外力F₁、F₂、・・・、Fᵢ、・・・Fₙが作用している状態を考え，この荷重に対応する各節点の変位をd₁、d₂、・・・、dᵢ、・・・dₙとする．

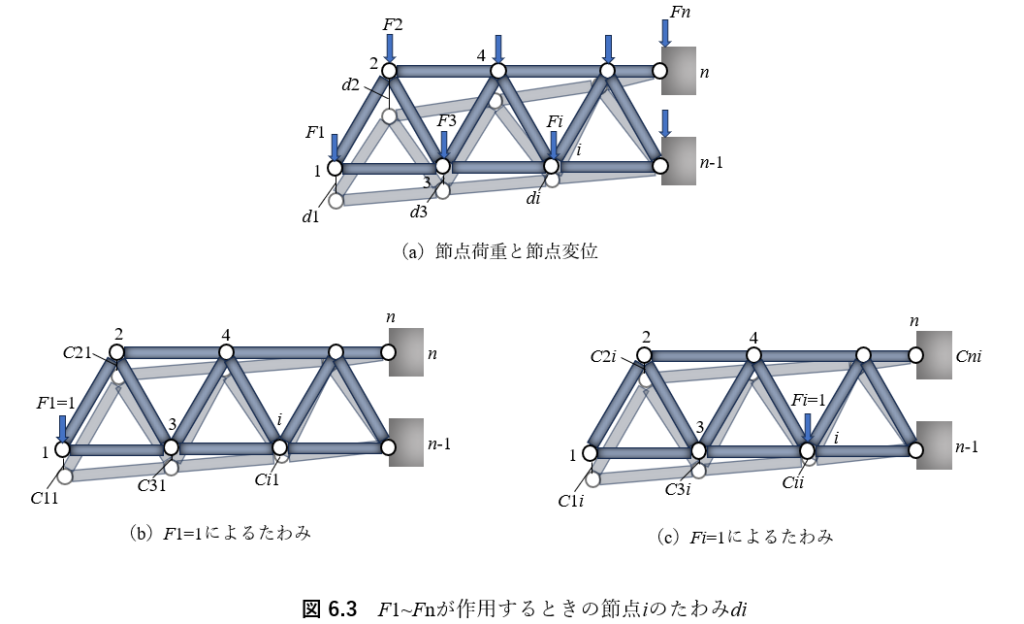
F₂とF₄が同時に作用するときのたわみν₃は、 F₂のみが作用したときのたわみν₃₂とF₄が同時に作用するときのたわみν₃は、F₂のみが作用したときのたわみν₃₂とF₄のみが作用したときのたわみν₃₄の和として求められる。

節点の変位に着目し、
F₁=1のみ作用するときの節点iの変位をCᵢ₁
F₂=1のみ作用するときの節点iの変位をCᵢ₂
Fᵢ=1のみ作用するときの節点iの変位をCᵢᵢ
などとすると、F₁、F₂、・・・、Fᵢ、・・・Fₙが同時に作用したときの節点iの変位 dᵢは、先に述べた線形性と重ね合せの原理により

dᵢ=Cᵢ₁F₁+Cᵢ₂F₂+・・・+CᵢᵢFᵢ+・・・+CᵢₙFₙ

と表すことができる。ほかの節点についても同様に考えられるから、上式にi= 1、2、、i、、n を代入すると、n個の方程式が得られる。これを行列 (マトリクス)で表すと

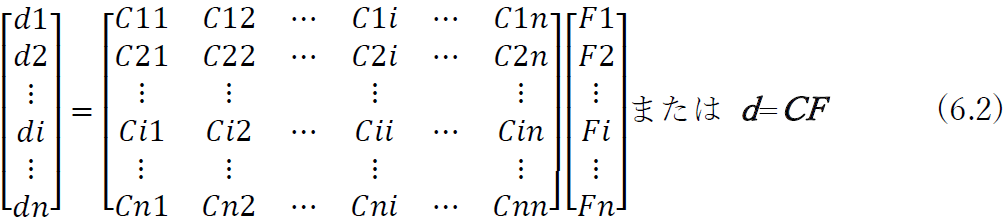
と書ける (行列の表記法と算法については, 次節にまとめている). これは,式 (5.17)で与えられた関数と類似のものである. Cil, Ci2, …, Cin は, 1~nの節点にはたらく単位荷重が点iの変位に及ぼす影響 (di の影響線値) を表しているので,この行列のことを変位影響係数マトリクスまたは撓性マトリクスとよぶ。 すべての係数 C11〜Cnn は,あらかじめ求めておけるから, 荷重 F1 ~ Fn が与えられると各点の変位 d1~dnを求めることができる.
一方，式 (6.2) n 元1次方程式であるから，F1~Fnについて解くこともでき，その結果は次のように表すことができる．

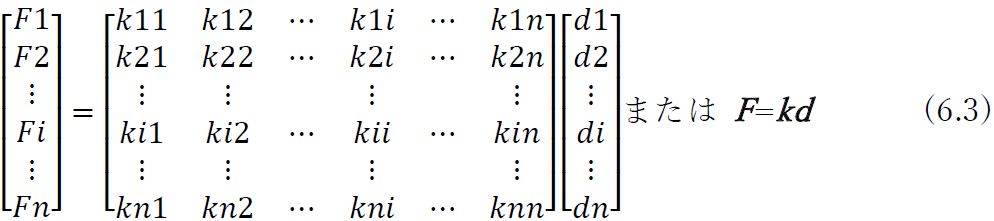
この行列の要素 kij の意味を考えるために, d1=1,d2 = d3 =・・・=dn=0 の場合に注目すると

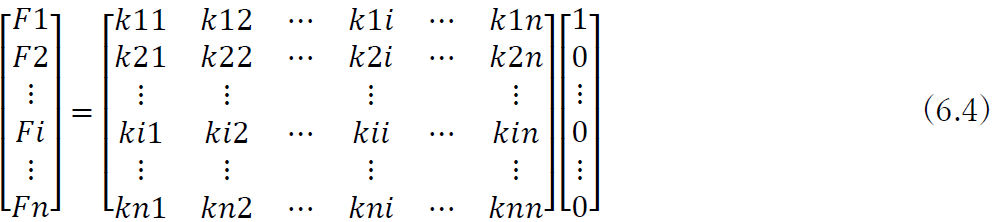
と書ける。右辺のかけ算を実行すると，Fi = ki1d1 = ki1 となる．これより，ki1 は，ほかの節点を動かないように固定して，節点1の変位のみを1だけ強制的に与えたときに,点に生じる力Fiの大きさを表していることがわかる．変位に対する抵抗 (剛性)が大きければ,力Fi (=ki1) も大きくなるので, ki1は構造物の剛性を表すことになる．そこで，この行列のことを剛性マトリクス (stiffness matrix) または剛性行列といい，式 (6.3) の形の表現のつり合い式を剛性方程式という．kij が，あらかじめ求められていれば，荷重 F1~Fn が与えられると各点の変位d1~ dn を求めることができる．
　以上のように，節点に作用する荷重と，対応する節点の変位との関係を行列表示して未知数を求める方法をマトリクス構造解析法という．